PythonにはJavaと同じ「オブジェクト指向」という概念があり、データと処理をまとめた「クラス」を定義し、その「クラス」から「インスタンス」を複数作成することができる。
また、Javaと同様にPythonでも、クラスの継承を行ったり、抽象メソッドを定義することもできる。
今回は、スーパークラス(親クラス)に、スケーリング(正規化・標準化等)を行う抽象メソッドと回帰直線を算出する処理を定義し、そのサブクラス(子クラス)で、スケーリング(正規化・標準化等)を行う処理を定義してみたので、そのサンプルプログラムを共有する。
なお、クラスの継承や抽象メソッドについての詳細は、以下のサイトを参照のこと。
https://smile-jsp.hateblo.jp/entry/2022/05/25/000000
スケーリング(標準化・正規化)を行う部分を抽象メソッドに定義した、回帰直線を算出するクラスのソースコードは、以下の通り。
import numpy as np
from abc import ABCMeta, abstractmethod
# metaclass=ABCMetaを指定することで抽象クラスになる
class OrigRegressionLineBase(metaclass=ABCMeta):
# クラス変数
eta = 0.001 # 学習率η
repeat_num = 10000 # 最急降下法の繰り返し回数
# 初期化処理
def __init__(self):
# 目的関数y=ax+bのa,bを求めるための初期値を宣言
# a,b(スケーリング後)を初期化
self.a_scl = 1
self.b_scl = 1
# a,b(スケーリング前)を初期化
self.a = 0
self.b = 0
# 与えられた入力データから、目的関数y=ax+bのa,b(スケーリング前)を算出する
def fit(self, data_x, data_y):
# 入力データをスケーリングする
input_data_x_scl = self.scaling(data_x)
input_data_y_scl = self.scaling(data_y)
# 最急降下法でa,b(スケーリング後)の値を算出
for num in range(OrigRegressionLineBase.repeat_num):
self.a_scl = self.a_scl - OrigRegressionLineBase.eta \
* self.__da_f(self.a_scl, self.b_scl, input_data_x_scl, input_data_y_scl)
self.b_scl = self.b_scl - OrigRegressionLineBase.eta \
* self.__db_f(self.a_scl, self.b_scl, input_data_x_scl, input_data_y_scl)
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の、a,bの値を算出
self.a = self.rev_scaling_a(self.a_scl, self.b_scl, data_x, data_y)
self.b = self.rev_scaling_b(self.a_scl, self.b_scl, data_x, data_y)
# 与えられたx座標から、y座標の予測値を返却する
def predict(self, data_x):
return self.a * data_x + self.b
# 入力データ(input_data)をスケーリングする抽象メソッド
# 具体的な処理はサブクラスで定義
@abstractmethod
def scaling(self, input_data):
pass
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の傾きaを算出する
# 具体的な処理はサブクラスで定義
@abstractmethod
def rev_scaling_a(self, a_scl, b_scl, input_data_x, input_data_y):
pass
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の切片bを算出する
# 具体的な処理はサブクラスで定義
@abstractmethod
def rev_scaling_b(self, a_scl, b_scl, input_data_x, input_data_y):
pass
# 最急降下法で利用するda_fを定義
# メソッド名の先頭に__を付与することで、プライベートメソッドとする
def __da_f(self, a, b, input_data_x, input_data_y):
ret = 0
input_data_cnt = len(input_data_x)
for tmp in range(input_data_cnt):
tmp_x = input_data_x[tmp][0]
tmp_y = input_data_y[tmp][0]
ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
return ret
# 最急降下法で利用するdb_fを定義
def __db_f(self, a, b, input_data_x, input_data_y):
ret = 0
input_data_cnt = len(input_data_x)
for tmp in range(input_data_cnt):
tmp_x = input_data_x[tmp][0]
tmp_y = input_data_y[tmp][0]
ret = ret + ( a * tmp_x + b - tmp_y ) / input_data_cnt
return ret
なお、回帰直線を算出する処理については、以下の記事を参照のこと。

また、先ほどのOrigRegressionLineBaseクラスのサブクラスで、スケーリング部分で標準化を行うクラスのソースコードは、以下の通り。
import numpy as np
class OrigRegressionLineStd(OrigRegressionLineBase):
# 入力データ(input_data)をスケーリングする抽象メソッドの具体的な処理
def scaling(self, input_data):
# 入力データの標準化を実施
ave_val = input_data.mean()
std_val = input_data.std()
if std_val == 0:
return []
else:
return (input_data - ave_val) / std_val
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の傾きaを算出する
# 抽象メソッドの具体的な処理
def rev_scaling_a(self, a_scl, b_scl, input_data_x, input_data_y):
# 入力データの値(スケーリング前)の標準偏差を算出
y_stdd = input_data_y.std()
x_stdd = input_data_x.std()
# 入力データの標準化戻し後の傾きaを算出する
return a_scl * y_stdd / x_stdd
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の切片bを算出する
# 抽象メソッドの具体的な処理
def rev_scaling_b(self, a_scl, b_scl, input_data_x, input_data_y):
# 入力データの値(スケーリング前)の平均・標準偏差を算出
x_ave = input_data_x.mean()
x_stdd = input_data_x.std()
y_ave = input_data_y.mean()
y_stdd = input_data_y.std()
# 入力データの標準化戻し後の切片bを算出する
return -a_scl * y_stdd * x_ave / x_stdd + b_scl * y_stdd + y_ave
なお、データを標準化した上で、回帰直線を算出する処理については、以下の記事を参照のこと。

さらに、OrigRegressionLineStdクラスのfitメソッドを呼び出してグラフ化した結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# 入力データのx座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# 入力データを訓練用とテスト用で分割
# test_sizeには、テストデータの割合を指定する
# random_stateを指定することで、分割方法を固定できる
train_data_x, test_data_x, train_data_y, test_data_y \
= train_test_split(input_data_x, input_data_y, test_size=0.2, random_state=0)
# OrigRegressionLineStdクラスを利用するため、抜き出したtrain_dataの
# x座標・y座標を、2次元1列の配列とする縦ベクトルに変更
train_data_x = train_data_x.reshape(-1, 1)
train_data_y = train_data_y.reshape(-1, 1)
# OrigRegressionLineStdクラスの回帰直線のa,bの値を算出
orls = OrigRegressionLineStd()
orls.fit(train_data_x, train_data_y)
print("*** a,bの値 ***")
print("a = " + str(orls.a) + ", b = " + str(orls.b))
# train_dataの値を散布図で表示
train_data_x = train_data_x.reshape(1, -1)
train_data_y = train_data_y.reshape(1, -1)
plt.scatter(input_data_x, input_data_y)
plt.title("train_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x = np.linspace(26, 36, 1000)
y = orls.a * x + orls.b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()
# test_dataの値を散布図で表示
test_data_x = test_data_x.reshape(1, -1)
test_data_y = test_data_y.reshape(1, -1)
plt.scatter(test_data_x, test_data_y)
plt.title("test_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x = np.linspace(26, 36, 1000)
y = orls.a * x + orls.b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()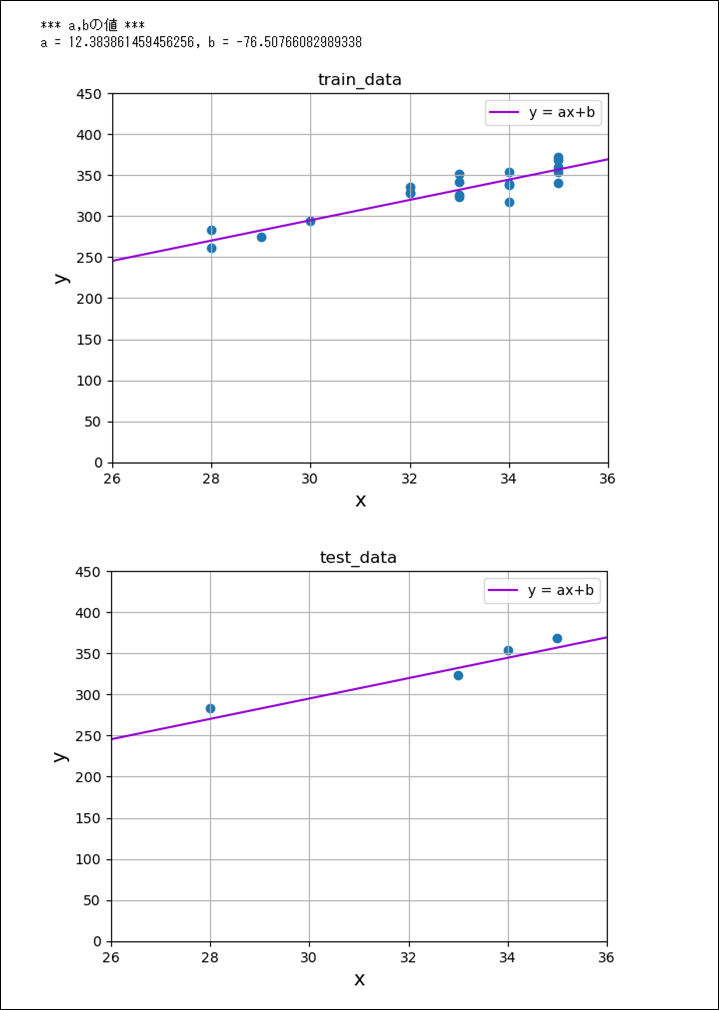
また、先ほどのOrigRegressionLineBaseクラスのサブクラスで、スケーリング部分で正規化を行うクラスのソースコードは、以下の通り。
import numpy as np
class OrigRegressionLineNorm(OrigRegressionLineBase):
# 入力データ(input_data)をスケーリングする抽象メソッドの具体的な処理
def scaling(self, input_data):
# 入力データの正規化を実施
input_data_cnt = len(input_data)
if input_data_cnt <= 0:
return []
max_val = input_data.max()
min_val = input_data.min()
if max_val == min_val:
return []
else:
return (input_data - min_val) / (max_val - min_val)
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の傾きaを算出する
# 抽象メソッドの具体的な処理
def rev_scaling_a(self, a_scl, b_scl, input_data_x, input_data_y):
# 入力データの値(スケーリング前)の最大値・最小値を算出
x_max = input_data_x.max()
x_min = input_data_x.min()
y_max = input_data_y.max()
y_min = input_data_y.min()
# 入力データの正規化戻し後の傾きaを算出する
return a_scl * (y_max - y_min) / (x_max - x_min)
# 算出した直線(y = a_scl * x + b_scl)をスケーリング戻し後の切片bを算出する
# 抽象メソッドの具体的な処理
def rev_scaling_b(self, a_scl, b_scl, input_data_x, input_data_y):
# 入力データの値(スケーリング前)の最大値・最小値を算出
x_max = input_data_x.max()
x_min = input_data_x.min()
y_max = input_data_y.max()
y_min = input_data_y.min()
# 入力データの正規化戻し後の切片bを算出する
return -a_scl * x_min * (y_max - y_min) / (x_max - x_min) + b_scl * (y_max - y_min) + y_min
なお、データを正規化した上で、回帰直線を算出する処理については、以下の記事を参照のこと。

さらに、OrigRegressionLineNormクラスのfitメソッドを呼び出してグラフ化した結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# 入力データのx座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# 入力データを訓練用とテスト用で分割
# test_sizeには、テストデータの割合を指定する
# random_stateを指定することで、分割方法を固定できる
train_data_x, test_data_x, train_data_y, test_data_y \
= train_test_split(input_data_x, input_data_y, test_size=0.2, random_state=0)
# OrigRegressionLineNormクラスを利用するため、抜き出したtrain_dataの
# x座標・y座標を、2次元1列の配列とする縦ベクトルに変更
train_data_x = train_data_x.reshape(-1, 1)
train_data_y = train_data_y.reshape(-1, 1)
# OrigRegressionLineNormクラスの回帰直線のa,bの値を算出
orls = OrigRegressionLineNorm()
orls.fit(train_data_x, train_data_y)
print("*** a,bの値 ***")
print("a = " + str(orls.a) + ", b = " + str(orls.b))
# train_dataの値を散布図で表示
train_data_x = train_data_x.reshape(1, -1)
train_data_y = train_data_y.reshape(1, -1)
plt.scatter(input_data_x, input_data_y)
plt.title("train_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x = np.linspace(26, 36, 1000)
y = orls.a * x + orls.b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()
# test_dataの値を散布図で表示
test_data_x = test_data_x.reshape(1, -1)
test_data_y = test_data_y.reshape(1, -1)
plt.scatter(test_data_x, test_data_y)
plt.title("test_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x = np.linspace(26, 36, 1000)
y = orls.a * x + orls.b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()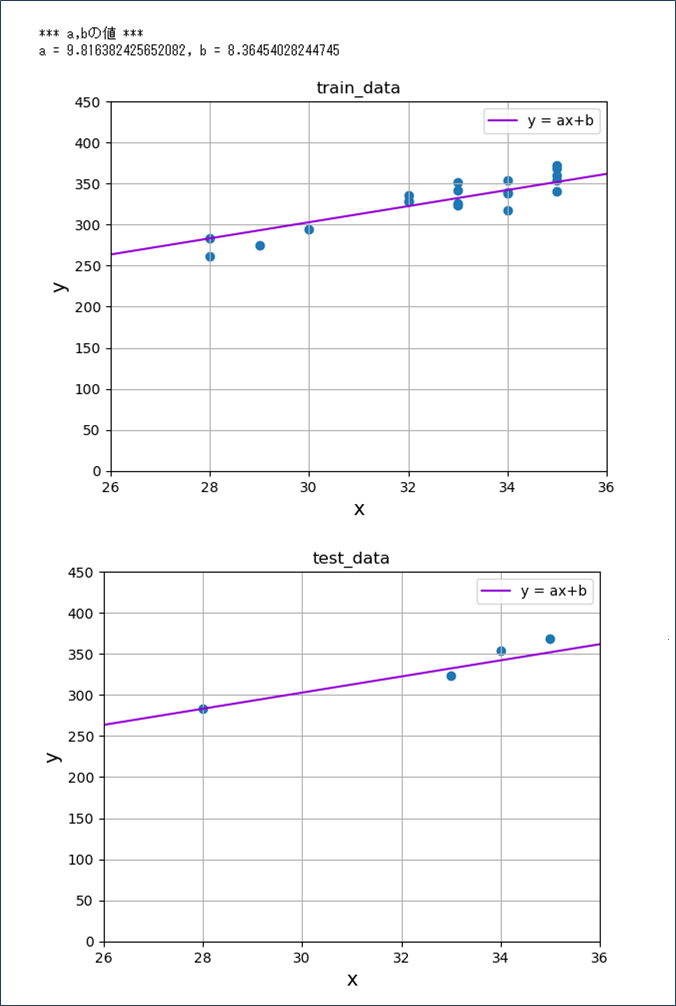
要点まとめ
- Javaと同様にPythonでも、クラスの継承を行ったり、抽象メソッドを定義することができる。





