重回帰分析を行うデータから重回帰式を算出してみた｜ITエンジニアとして経験・学習したこと

以下の記事で読み込んだデータを元に、住宅価格の最適解を求めることを考える。

重回帰分析を行うデータを読み込んでみた以下の「カリフォルニアの住宅価格データ」で、所得・築年数・部屋数・寝室数・人口・世帯人数・緯度・経度を元に、住宅価格を決めるモデルを...

上記記事では、\(y_{1}\)(MedHouseVal(住宅価格))の予測値\(\hat y_{1}\)を、以下の重回帰式で表現していた。
\[
\begin{eqnarray}
\hat y_{1} &=& x_{10}w_{0} + x_{11}w_{1} + x_{12}w_{2} + \ldots + x_{18}w_{8} \\
&=& \begin{pmatrix} x_{10} & x_{11} & x_{12} & \ldots & x_{18} \end{pmatrix} \begin{pmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{8} \end{pmatrix}
\end{eqnarray}
\]

これを一般化すると、\(N\)件のデータの予測値\(\boldsymbol{\hat y}\)は、行列\(X\), 縦ベクトル\(\boldsymbol w\)を利用して、以下の式で表せる。
\[
\begin{eqnarray}
\boldsymbol{\hat y} &=& \begin{pmatrix} x_{10} & x_{11} & x_{12} & \ldots & x_{18} \\
x_{20} & x_{21} & x_{22} & \ldots & x_{28} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \ldots & x_{N8} \end{pmatrix}
\begin{pmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{8} \end{pmatrix} = X \boldsymbol w
\end{eqnarray}
\]

上記\(\boldsymbol{\hat y}\)の最適解は、予測値と実際の値の差の2乗和が最小になる値（⇒最小2乗法）となる。予測値と実際の値の差の\(2\)乗和(\(L\))は、以下の式で表せる。
\[
\begin{eqnarray}
L &=& (y_{1} – {\hat y_{1}})^2 + (y_{2} – {\hat y_{2}})^2 + \ldots + (y_{N} – {\hat y_{N}})^2 \\
&=& \begin{pmatrix} y_{1} – {\hat y_{1}} & y_{2} – {\hat y_{2}} & \ldots & y_{N} – {\hat y_{N}} \end{pmatrix}
\begin{pmatrix} y_{1} – {\hat y_{1}} \\ y_{2} – {\hat y_{2}} \\ \vdots \\ y_{N} – {\hat y_{N}} \end{pmatrix}
= {}^t \!(\boldsymbol y – \boldsymbol{\hat y})(\boldsymbol y – \boldsymbol{\hat y})
\end{eqnarray}
\]

また、\(\boldsymbol{\hat y} = X \boldsymbol w\)、\({}^t\!(A + B) = {}^t \! A + {}^t \! B\)、\({}^t\!(AB) = {}^t \! B{}^t \! A\) なので、
\[
\begin{eqnarray}
L &=& {}^t \!(\boldsymbol y – \boldsymbol{\hat y})(\boldsymbol y – \boldsymbol{\hat y})
= {}^t \!(\boldsymbol y – X \boldsymbol w)(\boldsymbol y – X \boldsymbol w)
= ({}^t \!{\boldsymbol y} – {}^t \!(X \boldsymbol w))(\boldsymbol y – X \boldsymbol w) \\
&=& ({}^t \!{\boldsymbol y} – {}^t \!{\boldsymbol w}{}^t \!X)(\boldsymbol y – X \boldsymbol w)
= {}^t \!{\boldsymbol y}{\boldsymbol y} – {}^t \!{\boldsymbol y} X \boldsymbol w – {}^t \!{\boldsymbol w}{}^t \!X{\boldsymbol y} + {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w}
\end{eqnarray}
\]

なお、転置行列の公式については、以下のサイトを参照のこと。

転置行列の性質を確認してみた以下の記事で、転置行列の定義について記載している。 https://www.purin-it.com/python-numpy...

ここで、\({}^t \!{\boldsymbol y} X \boldsymbol w\)を計算すると、以下のようにスカラー(数値)となる。
\[
\begin{eqnarray}
{}^t \!{\boldsymbol y} X \boldsymbol w &=& \begin{pmatrix} y_{1} & y_{2} & \ldots & y_{N} \end{pmatrix}
\begin{pmatrix} x_{10} & x_{11} & x_{12} & \ldots & x_{18} \\
x_{20} & x_{21} & x_{22} & \ldots & x_{28} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & x_{N2} & \ldots & x_{N8} \end{pmatrix}
\begin{pmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{8} \end{pmatrix} \\
&=& \begin{pmatrix} y_{1} & y_{2} & \ldots & y_{N} \end{pmatrix}
\begin{pmatrix} x_{10}w_{0} + x_{11}w_{1} + x_{12}w_{2} + \ldots + x_{18}w_{8} \\
x_{20}w_{0} + x_{21}w_{1} + x_{22}w_{2} + \ldots + x_{28}w_{8} \\ \vdots \\
x_{N0}w_{0} + x_{N1}w_{1} + x_{N2}w_{2} + \ldots + x_{N8}w_{8} \end{pmatrix} \\
&=& \begin{pmatrix} y_{1} & y_{2} & \ldots & y_{N} \end{pmatrix}
\begin{pmatrix} \displaystyle \sum_{i=0}^{8}{x_{1i}w_{i}} \\ \displaystyle \sum_{i=0}^{8}{x_{2i}w_{i}} \\
\vdots \\ \displaystyle \sum_{i=0}^{8}{x_{Ni}w_{i}} \end{pmatrix} \\
&=& y_{1}\displaystyle \sum_{i=0}^{8}{x_{1i}w_{i}} + y_{2}\displaystyle \sum_{i=0}^{8}{x_{2i}w_{i}} + \ldots + y_{N}\displaystyle \sum_{i=0}^{8}{x_{Ni}w_{i}}
= \displaystyle \sum_{k=1}^{N}y_{k} \left( \sum_{i=0}^{8}{x_{ki}w_{i}} \right)
\end{eqnarray}
\]

そのため、転置しても同じ値となる。また、\({}^t\!(AB) = {}^t \! B{}^t \! A\)、\({}^t\!(ABC) = {}^t\!((AB)C) = {}^t \! C{}^t \! (AB) = {}^t \! C{}^t \! B{}^t \! A\)、\({}^t \!({}^t \! A) = A\) なので、
\[
\begin{eqnarray}
{}^t \!{\boldsymbol y} X \boldsymbol w = {}^t \!({}^t \!{\boldsymbol y} X \boldsymbol w)
= {}^t \!{\boldsymbol w} {}^t \! X {}^t \!({}^t \!{\boldsymbol y}) = {}^t \!{\boldsymbol w} {}^t \! X \boldsymbol y
\end{eqnarray}
\]

そうすると、\(L\)は以下のように式変形できる。
\[
\begin{eqnarray}
L &=& {}^t \!{\boldsymbol y}{\boldsymbol y} – {}^t \!{\boldsymbol y} X \boldsymbol w – {}^t \!{\boldsymbol w}{}^t \!X{\boldsymbol y} + {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w}
= {}^t \!{\boldsymbol y}{\boldsymbol y} – {}^t \!{\boldsymbol y} X \boldsymbol w – {}^t \!{\boldsymbol y} X \boldsymbol w + {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w} \\
&=& {}^t \!{\boldsymbol y}{\boldsymbol y} – 2{}^t \!{\boldsymbol y} X \boldsymbol w + {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w}
= {}^t \!{\boldsymbol y}{\boldsymbol y} – 2{}^t \!({}^t \! X \boldsymbol y) \boldsymbol w + {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w}
\end{eqnarray}
\]

ここで、\({}^t \! X \boldsymbol y\)を計算すると、以下のように縦ベクトルとなる。
\[
\begin{eqnarray}
{}^t \! X \boldsymbol y &=& \begin{pmatrix} x_{10} & x_{20} & \ldots & x_{N0} \\
x_{11} & x_{21} & \ldots & x_{N1} \\
\vdots & \vdots & \ddots & \vdots \\
x_{18} & x_{28} & \ldots & x_{N8} \end{pmatrix}
\begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{pmatrix} \\
&=& \begin{pmatrix} x_{10}y_{1} + x_{20}y_{2} + \ldots + x_{N0}y_{N} \\
x_{11}y_{1} + x_{21}y_{2} + \ldots + x_{N1}y_{N} \\ \vdots \\
x_{18}y_{1} + x_{28}y_{2} + \ldots + x_{N8}y_{N} \end{pmatrix}
= \begin{pmatrix} \displaystyle \sum_{i=1}^{N}x_{i0}y_{i} \\ \displaystyle \sum_{i=1}^{N}x_{i1}y_{i} \\
\vdots \\ \displaystyle \sum_{i=1}^{N}x_{i8}y_{i} \end{pmatrix}
\end{eqnarray}
\]

また、\({}^t \!XX\)を計算すると、以下のように行列となる。
\[
\begin{eqnarray}
{}^t \!XX &=& \begin{pmatrix} x_{10} & x_{20} & \ldots & x_{N0} \\
x_{11} & x_{21} & \ldots & x_{N1} \\
\vdots & \vdots & \ddots & \vdots \\
x_{18} & x_{28} & \ldots & x_{N8} \end{pmatrix}
\begin{pmatrix} x_{10} & x_{11} & \ldots & x_{18} \\
x_{20} & x_{21} & \ldots & x_{28} \\
\vdots & \vdots & \ddots & \vdots \\
x_{N0} & x_{N1} & \ldots & x_{N8} \end{pmatrix} \\
&=& \begin{pmatrix} x_{10}x_{10} + x_{20}x_{20} + \ldots + x_{N0}x_{N0} & x_{10}x_{11} + x_{20}x_{21} + \ldots + x_{N0}x_{N1}
& \ldots & x_{10}x_{18} + x_{20}x_{28} + \ldots + x_{N0}x_{N8} \\
x_{11}x_{10} + x_{21}x_{20} + \ldots + x_{N1}x_{N0} & x_{11}x_{11} + x_{21}x_{21} + \ldots + x_{N1}x_{N1}
& \ldots & x_{11}x_{18} + x_{21}x_{28} + \ldots + x_{N1}x_{N8} \\ \vdots & \vdots & \ddots & \vdots \\
x_{18}x_{10} + x_{28}x_{20} + \ldots + x_{N8}x_{N0} & x_{18}x_{11} + x_{28}x_{21} + \ldots + x_{N8}x_{N1}
& \ldots & x_{18}x_{18} + x_{28}x_{28} + \ldots + x_{N8}x_{N8} \end{pmatrix} \\
&=& \begin{pmatrix} \displaystyle \sum_{i=1}^{N}x_{i0}x_{i0} & \displaystyle \sum_{i=1}^{N}x_{i0}x_{i1} & \ldots & \displaystyle \sum_{i=1}^{N}x_{i0}x_{i8} \\
\displaystyle \sum_{i=1}^{N}x_{i1}x_{i0} & \displaystyle \sum_{i=1}^{N}x_{i1}x_{i1} & \ldots & \displaystyle \sum_{i=1}^{N}x_{i1}x_{i8} \\
\vdots & \vdots & \ddots & \vdots \\
\displaystyle \sum_{i=1}^{N}x_{i8}x_{i0} & \displaystyle \sum_{i=1}^{N}x_{i8}x_{i1} & \ldots & \displaystyle \sum_{i=1}^{N}x_{i8}x_{i8} \end{pmatrix}
\end{eqnarray}
\]

そのため、\({}^t \! X \boldsymbol y = \boldsymbol b\)、\({}^t \!XX = A\)と置き換えると、\(L\)は以下のように式変形できる。
\[
\begin{eqnarray}
L = {}^t \!{\boldsymbol y}{\boldsymbol y} – 2{}^t \!({}^t \! X \boldsymbol y) \boldsymbol w + {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w}
= {}^t \!{\boldsymbol y}{\boldsymbol y} – 2{}^t \!{\boldsymbol b} \boldsymbol w + {}^t \!{\boldsymbol w}A{\boldsymbol w}
\end{eqnarray}
\]

「AOMEI Partition Assistant Standard(無料)版」は便利なパーティション管理ツールだったハードディスクの記憶領域を論理的に分割し、分割された個々の領域のことを、パーティションといいます。例えば、以下の図の場合、C/D...

ここで、以下の計算結果より、\({}^t \!{\boldsymbol y}{\boldsymbol y}\)は定数、\(2{}^t \!{\boldsymbol b} \boldsymbol w = 2{}^t \!({}^t \! X \boldsymbol y) \boldsymbol w\)は\(w_{i}\)について\(1\)次関数、\({}^t \!{\boldsymbol w}A{\boldsymbol w} = {}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w} \)は\(w_{i}\)について\(2\)次関数となるため、\(L\)は\(w_{i}\)について(下に凸の)\(2\)次関数となる。
\[
\begin{eqnarray}
{}^t \!{\boldsymbol y}{\boldsymbol y} &=& \begin{pmatrix} y_{1} & y_{2} & \ldots & y_{N} \end{pmatrix}\begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{pmatrix}
= {y_{1}}^2 + {y_{2}}^2 + \ldots + {y_{N}}^2 = \displaystyle \sum_{i=1}^{N}{y_{i}}^2 \\
2{}^t \!({}^t \! X \boldsymbol y) \boldsymbol w &=& 2\begin{pmatrix} \displaystyle \sum_{i=1}^{N}x_{i0}y_{i} & \displaystyle \sum_{i=1}^{N}x_{i1}y_{i} &
\ldots & \displaystyle \sum_{i=1}^{N}x_{i8}y_{i} \end{pmatrix}
\begin{pmatrix} w_{0} \\ w_{1} \\ \vdots \\ w_{8} \end{pmatrix} \\
&=& 2w_{0}\displaystyle \sum_{i=1}^{N}x_{i0}y_{i} + 2w_{1}\displaystyle \sum_{i=1}^{N}x_{i1}y_{i} + \ldots + 2w_{8}\displaystyle \sum_{i=1}^{N}x_{i8}y_{i} \\
{}^t \!{\boldsymbol w}{}^t \!XX{\boldsymbol w} &=& \begin{pmatrix} w_{0} & w_{1} & \ldots & w_{8} \end{pmatrix}
\begin{pmatrix} \displaystyle \sum_{i=1}^{N}x_{i0}x_{i0} & \displaystyle \sum_{i=1}^{N}x_{i0}x_{i1} & \ldots & \displaystyle \sum_{i=1}^{N}x_{i0}x_{i8} \\
\displaystyle \sum_{i=1}^{N}x_{i1}x_{i0} & \displaystyle \sum_{i=1}^{N}x_{i1}x_{i1} & \ldots & \displaystyle \sum_{i=1}^{N}x_{i1}x_{i8} \\
\vdots & \vdots & \ddots & \vdots \\
\displaystyle \sum_{i=1}^{N}x_{i8}x_{i0} & \displaystyle \sum_{i=1}^{N}x_{i8}x_{i1} & \ldots & \displaystyle \sum_{i=1}^{N}x_{i8}x_{i8} \end{pmatrix}
\begin{pmatrix} w_{0} \\ w_{1} \\ \vdots \\ w_{8} \end{pmatrix} \\
&=& \begin{pmatrix} w_{0} & w_{1} & \ldots & w_{8} \end{pmatrix}
\begin{pmatrix} w_{0}\displaystyle \sum_{i=1}^{N}x_{i0}x_{i0} + w_{1}\displaystyle \sum_{i=1}^{N}x_{i0}x_{i1}
+ \ldots + w_{8}\displaystyle \sum_{i=1}^{N}x_{i0}x_{i8} \\
w_{0}\displaystyle \sum_{i=1}^{N}x_{i1}x_{i0} + w_{1}\displaystyle \sum_{i=1}^{N}x_{i1}x_{i1}
+ \ldots + w_{8}\displaystyle \sum_{i=1}^{N}x_{i1}x_{i8} \\ \vdots \\
w_{0}\displaystyle \sum_{i=1}^{N}x_{i8}x_{i0} + w_{1}\displaystyle \sum_{i=1}^{N}x_{i8}x_{i1}
+ \ldots + w_{8}\displaystyle \sum_{i=1}^{N}x_{i8}x_{i8} \end{pmatrix} \\
&=& {w_{0}}^2\displaystyle \sum_{i=1}^{N}x_{i0}x_{i0} + {w_{1}}^2\displaystyle \sum_{i=1}^{N}x_{i1}x_{i1} + \ldots
+ {w_{8}}^2\displaystyle \sum_{i=1}^{N}x_{i8}x_{i8} + \ldots
\end{eqnarray}
\]

(下に凸の)\(2\)次関数における最小値では、以下のグラフのように、傾き\(=0\)になる。

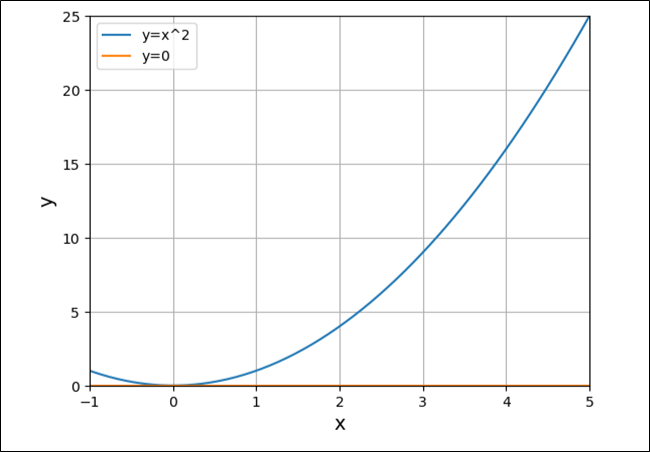
そのため、\(L\)(予測値と実際の値の差の2乗和が最小になる値)が最小になる値は、\(L\)を\(\boldsymbol w\)について偏微分して\(0\)になる値を算出すればよい。そこで、\(L\)を\(\boldsymbol w\)について偏微分すると、
\[
\begin{eqnarray}
\displaystyle \frac{\partial L}{\partial {\boldsymbol w}}
= \frac{\partial}{\partial {\boldsymbol w}}({}^t \!{\boldsymbol y}{\boldsymbol y} – 2{}^t \!{\boldsymbol b} \boldsymbol w + {}^t \!{\boldsymbol w}A{\boldsymbol w})
= \frac{\partial}{\partial {\boldsymbol w}}({}^t \!{\boldsymbol y}{\boldsymbol y})
– 2\frac{\partial}{\partial {\boldsymbol w}}({}^t \!{\boldsymbol b} \boldsymbol w)
+ \frac{\partial}{\partial {\boldsymbol w}}({}^t \!{\boldsymbol w}A{\boldsymbol w})
\end{eqnarray}
\]

ここで、\(\displaystyle \frac{\partial}{\partial \boldsymbol x} \left( c \right) = \boldsymbol 0\)、\(\displaystyle \frac{\partial}{\partial \boldsymbol x} \left( {}^t \! \boldsymbol a \boldsymbol x \right) = \boldsymbol a\)、\(\displaystyle \frac{\partial}{\partial \boldsymbol x} \left( {}^t \! \boldsymbol x A \boldsymbol x \right) = (A + {}^t \! A)\boldsymbol x\) なので、
\[
\begin{eqnarray}
\displaystyle \frac{\partial L}{\partial {\boldsymbol w}} = {\boldsymbol 0} – 2{\boldsymbol b} + (A + {}^t \! A)\boldsymbol w = – 2{\boldsymbol b} + (A + {}^t \! A)\boldsymbol w
\end{eqnarray}
\]

なお、ベクトル微分の公式については、以下のサイトを参照のこと。

ベクトル微分の公式を確認してみた行列のうち、\(m\)行\(1\)列のものを「列ベクトル」という。\(\boldsymbol x\)と\(\boldsymbol a...

さらに、\(\boldsymbol b = {}^t \! X \boldsymbol y\)、\(A = {}^t \!XX\)を戻し、\({}^t\!(AB) = {}^t \! B{}^t \! A\)、\({}^t \!({}^t \! A) = A\)なので、
\[
\begin{eqnarray}
\displaystyle \frac{\partial L}{\partial {\boldsymbol w}} &=& – 2{\boldsymbol {}^t \! X \boldsymbol y} + ({}^t \!XX + {}^t \! ({}^t \!XX))\boldsymbol w
= – 2{\boldsymbol {}^t \! X \boldsymbol y} + ({}^t \!XX + {}^t \!X {}^t \!({}^t \!X)) \boldsymbol w \\
&=& – 2{\boldsymbol {}^t \! X \boldsymbol y} + ({}^t \!XX + {}^t \!XX) \boldsymbol w = – 2{\boldsymbol {}^t \! X \boldsymbol y} + 2{}^t \!XX \boldsymbol w
\end{eqnarray}
\]

\(\displaystyle \frac{\partial L}{\partial {\boldsymbol w}}\)が\(\boldsymbol 0\)になればよいので、
\[
\begin{eqnarray}
– 2{\boldsymbol {}^t \! X \boldsymbol y} + 2{}^t \!XX \boldsymbol w &=& \boldsymbol 0 \\
2{}^t \!XX \boldsymbol w &=& 2{\boldsymbol {}^t \! X \boldsymbol y} \\
{}^t \!XX \boldsymbol w &=& \boldsymbol {}^t \! X \boldsymbol y
\end{eqnarray}
\]

\({}^t \!XX\)が正方行列で、逆行列\(({}^t \!XX)^{-1}\)を計算できることから、両辺に左から\(({}^t \!XX)^{-1}\)を掛けて、
\[
\begin{eqnarray}
({}^t \!XX)^{-1}{}^t \!XX \boldsymbol w &=& ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y \\
I\boldsymbol w &=& ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y \\
\boldsymbol w &=& ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y
\end{eqnarray}
\]

以上より、\(N\)件のデータの予測値\(\boldsymbol{\hat y}\)の最適解は、上記\(\boldsymbol w = ({}^t \!XX)^{-1}\boldsymbol {}^t \! X \boldsymbol y\)を利用して算出すればよい。