以下の記事で、ロジスティック回帰分析に従う、アヤメがvirginicaである確率\(p\)の計算式を算出してきた。

上記記事で算出した確率\(p\)の計算式は、petal length (cm)を\(\mathrm{pl}\)、petal width (cm)を\(\mathrm{pw}\)と記載すると、以下の通り。
\[
\begin{eqnarray}
p &=& \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \\\\
p &:& アヤメが\mathrm{virginica}である確率 \\
B &:& 条件0(\mathrm{pl}<5、かつ、\mathrm{pw}<1.7)のオッズ \\
A_1 &:& (条件0に対する)条件1(\mathrm{pl}≧5)のオッズ比 \\
x_1 &:& (条件1に対する)0か1の値 \\
A_2 &:& (条件0に対する)条件2(\mathrm{pw}≧1.7)のオッズ比 \\
x_2 &:& (条件2に対する)0か1の値 \\
b &:& \log B \\
a_1 &:& \log A_1 \\
a_2 &:& \log A_2
\end{eqnarray}
\]
また、以下の記事では、ロジスティクス回帰分析の尤度関数の最適解の算出を行い、アヤメがvirginicaかどうか判定するクラスを自前で作成していた。

上記記事の実装は、Python で利用できるデータ分析や機械学習のためのライブラリの一つであるscikit-learnを用いて行うこともできる。
今回は、scikit-learnのLogisticRegressionクラスを用いて、アヤメがvirginicaかどうか判定してみたので、そのサンプルプログラムを共有する。
LogisticRegressionクラスを用いて、アヤメがvirginicaかどうかを判定した結果は以下の通りで、正常に判定できていることが確認できる。
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
# アヤメのデータセットのデータを取得
iris = load_iris()
# 先頭51~55件目のデータ(versicolor)と、先頭101~105件目のデータ(virginica)の
# データを結合し、X1に格納
X1 = np.append(iris.data[50:55], iris.data[100:105], axis=0)
print("*** 結合した先頭51~55件目と先頭101~105件目のデータ ***")
print(X1)
print()
# 先頭51~55件目のデータ(versicolor)と、先頭101~105件目のデータ(virginica)の
# データを結合し、petal length(cm), petal width(cm)のみ抽出したデータをX2に格納
X2 = np.append(iris.data[50:55, -2:], iris.data[100:105, -2:], axis=0)
print("*** 結合した先頭51~55件目と先頭101~105件目のデータ ***")
print("*** petal length(cm), petal width(cm)のみ抽出 ***")
print(X2)
print()
# 先頭51~55件目の結果(versicolor)と、先頭101~105件目の結果(virginica)の
# データを結合し、yに格納
y = np.append(iris.target[50:55], iris.target[100:105], axis=0)
# 先頭51~55件目と先頭101~105件目の結果
print("*** 先頭51~55件目の結果 ***")
print(iris.target[50:55])
print("*** 先頭101~105件目の結果 ***")
print(iris.target[100:105])
print()
# scikit-learnのLogisticRegressionに適用
lr = LogisticRegression()
lr.fit(X2, y)
# LogisticRegressionによる算出結果
print("*** petal length(cm), petal width(cm)のみ抽出したデータからの判定 ***")
print("*** 先頭51~55件目のデータから判定した結果 ***")
print(lr.predict(iris.data[50:55, -2:]))
print("*** 先頭101~105件目のデータから判定した結果 ***")
print(lr.predict(iris.data[100:105, -2:]))

また、LogisticRegressionクラスを用いて、アヤメがvirginicaかどうかを判定する際に作成した学習済モデルの重みと切片を確認した結果は、以下の通り。
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
# アヤメのデータセットのデータを取得
iris = load_iris()
# 先頭51~55件目のデータ(versicolor)と、先頭101~105件目のデータ(virginica)の
# データを結合し、X1に格納
X1 = np.append(iris.data[50:55], iris.data[100:105], axis=0)
# 先頭51~55件目のデータ(versicolor)と、先頭101~105件目のデータ(virginica)の
# データを結合し、petal length(cm), petal width(cm)のみ抽出したデータをX2に格納
X2 = np.append(iris.data[50:55, -2:], iris.data[100:105, -2:], axis=0)
print("*** 結合した先頭51~55件目と先頭101~105件目のデータ ***")
print("*** petal length(cm), petal width(cm)のみ抽出 ***")
print(X2)
print()
# 先頭51~55件目の結果(versicolor)と、先頭101~105件目の結果(virginica)の
# データを結合し、yに格納
y = np.append(iris.target[50:55], iris.target[100:105], axis=0)
# scikit-learnのLogisticRegressionに適用
lr = LogisticRegression()
lr.fit(X2, y)
# LogisticRegressionの重み・切片の値
print("*** LogisticRegressionで作成済モデルの重み・切片を確認 ***")
print("*** 重み(coef_) ***")
print(lr.coef_)
print("*** 切片(intercept_) ***")
print(lr.intercept_)
上記で算出された重みと切片を、\(p = \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }}\)における変数と対応させると、\(b=-8.01317628\)(=切片)、\(a_1=1.29841591\)(=重みの1番目の要素)、\(a_2=0.78519427\)(=重みの2番目の要素)となり、\(x_1\)は(入力データの)petal length(cm)、\(x_2\)は(入力データの)petal width(cm)となる。
実際に、各入力データに対する確率\(p\)を計算した結果は以下の通りで、先頭51~55件目のデータの確率\(p≦0.5\)で、先頭101~105件目のデータの確率\(p>0.5\)であることが確認できる。
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
# アヤメのデータセットのデータを取得
iris = load_iris()
# 先頭51~55件目のデータ(versicolor)と、先頭101~105件目のデータ(virginica)の
# データを結合し、X1に格納
X1 = np.append(iris.data[50:55], iris.data[100:105], axis=0)
# 先頭51~55件目のデータ(versicolor)と、先頭101~105件目のデータ(virginica)の
# データを結合し、petal length(cm), petal width(cm)のみ抽出したデータをX2に格納
X2 = np.append(iris.data[50:55, -2:], iris.data[100:105, -2:], axis=0)
# 先頭51~55件目の結果(versicolor)と、先頭101~105件目の結果(virginica)の
# データを結合し、yに格納
y = np.append(iris.target[50:55], iris.target[100:105], axis=0)
# scikit-learnのLogisticRegressionに適用
lr = LogisticRegression()
lr.fit(X2, y)
# LogisticRegressionの重み・切片の値
print("*** LogisticRegressionで作成済モデルの重み・切片を確認 ***")
print("*** 重み(coef_) ***")
print(lr.coef_)
print("*** 切片(intercept_) ***")
print(lr.intercept_)
print()
print("*** 確率pを計算した結果 ***")
for x in X2:
u = lr.intercept_[0] + lr.coef_[0][0] * x[0] + lr.coef_[0][1] * x[1]
p = 1 / (1 + np.exp(-u))
print("入力データ:" + str(x) + "、確率p:" + str(p) + "、確率p>0.5?:" + str(p > 0.5))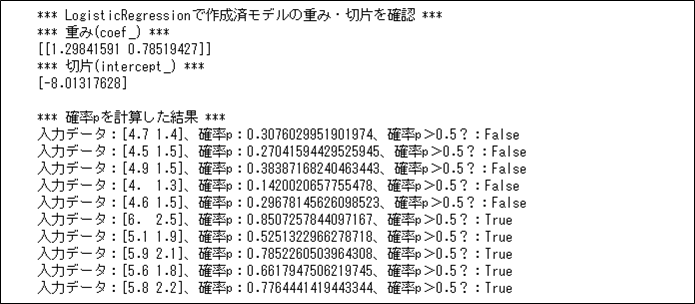
要点まとめ
- Python で利用できるデータ分析や機械学習のためのライブラリの一つとして、scikit-learnがある。
- ロジスティック回帰分析の確率\(p\)の最適解算出や2値分類は、scikit-learnのLogisticRegressionクラスを利用して実施できる。





