ニューラルネットワークの誤差関数の微分を計算してみた｜ITエンジニアとして経験・学習したこと

以下の記事で、ニューラルネットワークのフォワードプロパゲーションによる出力値\(y\)を算出してきたが、その際、重み\(\boldsymbol w\)に固定値を指定していた。

ニューラルネットワークのフォワードプロパゲーションを実装してみたニューラルネットワークは、人間の脳の神経細胞（ニューロン）の仕組みをプログラム上で模したモデルで、機械学習の1手法であるディープラー...

今回は、バックプロパゲーション（最急降下法を用いて、ニューラルネットワークの誤差を効率的に逆伝播させる手法）により、重み\(\boldsymbol w\)の最適解を求めることを考える。

なお、バックプロパゲーションについては、以下のサイトを参照のこと。
https://reinforz.co.jp/bizmedia/5656/

重み\(\boldsymbol w\)の最適解は、下図における誤差関数\(E=(x_3 – y)^2\)が最小となる箇所で、これは誤差関数を（桃枠の）重みの各変数について偏微分した結果が\(0\)になる値となる。

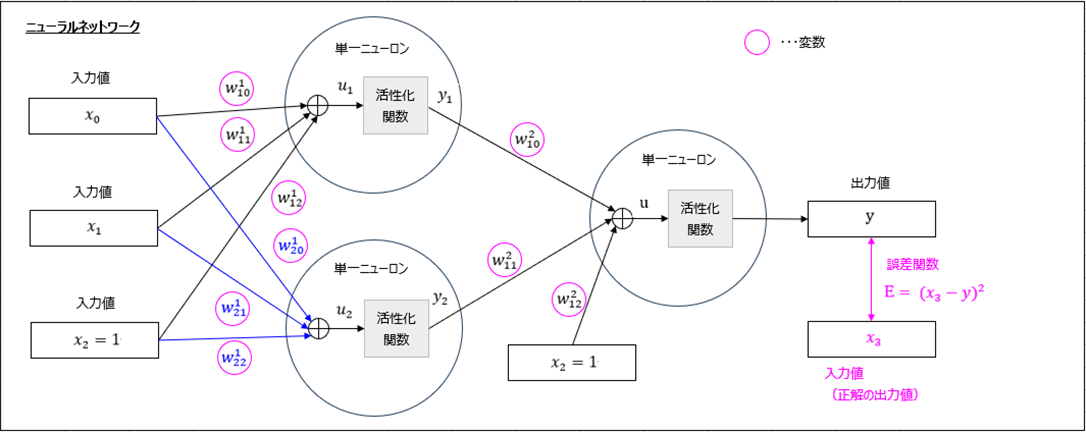
誤差関数を、重みの各変数についての偏微分する際、活性化関数にはシグモイド関数を利用すると共に、以下の計算結果も利用するものとする。
\[
\begin{eqnarray}
u_1 &=& x_0 \times w^1_{10} + x_1 \times w^1_{11} + 1 \times w^1_{12} \\
y_1 &=& \displaystyle \frac{1}{1 + e^{-u_1}} \\
u_2 &=& x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22} \\
y_2 &=& \displaystyle \frac{1}{1 + e^{-u_2}} \\
u &=& y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12} \\
y &=& \displaystyle \frac{1}{1 + e^{-u}}
\end{eqnarray}
\]

実際に、誤差関数を、重みの各変数についての偏微分を計算した結果は、以下の通り。
\[
\begin{multline}
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{10}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_1}
\frac{\partial y_1}{\partial u_1} \frac{\partial u_1}{\partial w^1_{10}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial y_1}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　　\times \frac{\partial}{\partial u_1}\frac{1}{1 + e^{-u_1}} \times
\frac{\partial}{\partial w^1_{10}}(x_0 \times w^1_{10} + x_1 \times w^1_{11} + 1 \times w^1_{12}) } \\
\shoveleft{　　　= 2(x_3 – y) \times (-1) \times u(1 – u) \times w^2_{10} \times u_1(1 – u_1) \times x_0 } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{10} \times u_1(1 – u_1) \times x_0 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{11}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_1}
\frac{\partial y_1}{\partial u_1} \frac{\partial u_1}{\partial w^1_{11}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial y_1}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　　\times \frac{\partial}{\partial u_1}\frac{1}{1 + e^{-u_1}} \times
\frac{\partial}{\partial w^1_{11}}(x_0 \times w^1_{10} + x_1 \times w^1_{11} + 1 \times w^1_{12}) } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{10} \times u_1(1 – u_1) \times x_1 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{12}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_1}
\frac{\partial y_1}{\partial u_1} \frac{\partial u_1}{\partial w^1_{12}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial y_1}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　　\times \frac{\partial}{\partial u_1}\frac{1}{1 + e^{-u_1}} \times
\frac{\partial}{\partial w^1_{12}}(x_0 \times w^1_{10} + x_1 \times w^1_{11} + 1 \times w^1_{12}) } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{10} \times u_1(1 – u_1) \times 1 } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{10} \times u_1(1 – u_1) } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{20}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_2}
\frac{\partial y_2}{\partial u_2} \frac{\partial u_2}{\partial w^1_{20}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial y_2}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　　\times \frac{\partial}{\partial u_2}\frac{1}{1 + e^{-u_2}} \times
\frac{\partial}{\partial w^1_{20}}(x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22}) } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{11} \times u_2(1 – u_2) \times x_0 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{21}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_2}
\frac{\partial y_2}{\partial u_2} \frac{\partial u_2}{\partial w^1_{21}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial y_2}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　　\times \frac{\partial}{\partial u_2}\frac{1}{1 + e^{-u_2}} \times
\frac{\partial}{\partial w^1_{21}}(x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22}) } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{11} \times u_2(1 – u_2) \times x_1 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{22}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_2}
\frac{\partial y_2}{\partial u_2} \frac{\partial u_2}{\partial w^1_{22}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial y_2}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　　\times \frac{\partial}{\partial u_2}\frac{1}{1 + e^{-u_2}} \times
\frac{\partial}{\partial w^1_{22}}(x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22}) } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{11} \times u_2(1 – u_2) \times 1 } \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times w^2_{11} \times u_2(1 – u_2)} \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^2_{10}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w^2_{10}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial w^2_{10}}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times y_1} \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^2_{11}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w^2_{11}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial w^2_{11}}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times y_2} \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^2_{12}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w^2_{12}} } \\
\shoveleft{　　　= \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\frac{1}{1 + e^{-u}}
\times \frac{\partial}{\partial w^2_{12}}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u) \times 1} \\
\shoveleft{　　　= 2(y – x_3) \times u(1 – u)}
\end{multline}
\]