以下の式で表現される関数をReLU関数といい、ディープラーニングの活性化関数の1つとして利用される。
\[
\begin{eqnarray}
f(x) = \left\{ \begin{array}{l} 0 （x＜0の場合）\\ x （x≧0の場合）\end{array} \right.
\end{eqnarray}
\]
以前ご紹介した「シグモイド関数」を、ニューラルネットワークの中間層の活性化関数に利用すると、以下のサイトに記載の「勾配消失問題」が発生しやすくなる。
https://zero2one.jp/ai-word/vanishing-gradient-problem/
この「勾配消失問題」の発生を防ぐため、ニューラルネットワークの中間層の活性化関数に「ReLU関数」がよく使われる。
今回は、ReLU関数とその微分をグラフ化してみたので、その結果を共有する。
\(f(x)=\left\{ \begin{array}{l} 0 （x＜0の場合）\\ x （x≧0の場合）\end{array} \right.\)をPythonでグラフ化した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # ReLU関数の定義 def relu(x): return np.where(x < 0, 0, x) # -10～10までを1000等分した値をxとする x = np.linspace(-10, 10, 1000) # 上記xに対応するReLU関数yの値を算出 y = relu(x) # x,yに対応する値のグラフを表示 plt.plot(x, y) plt.title("ReLU function") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.grid() plt.show() |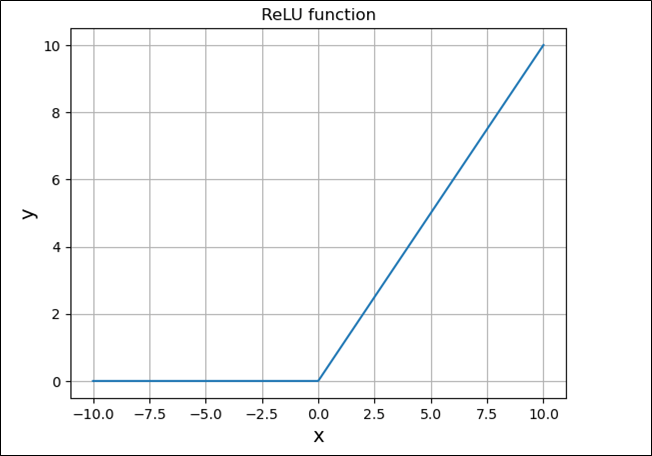
また、\(f(x)=\left\{ \begin{array}{l} 0 （x＜0の場合）\\ x （x≧0の場合）\end{array} \right.\)を\(x\)について微分すると、
\(\displaystyle \frac{d}{dx}f(x) = \left\{ \begin{array}{l} \displaystyle \frac{d}{dx}0=0 （x＜0の場合）\\ \displaystyle \frac{d}{dx}x=1 （x≧0の場合）\end{array} \right.\)となる。
上記、ReLU関数の微分をグラフに追加した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # ReLU関数の定義 def relu(x): return np.where(x < 0, 0, x) # ReLU関数の微分の定義 def diff_relu(x): return np.where(x < 0, 0, 1) # -10～10までを1000等分した値をxとする x = np.linspace(-10, 10, 1000) # 上記xに対応するReLU関数y1の値を算出 y1 = relu(x) # 上記xに対応するReLU関数の微分y2の値を算出 y2 = diff_relu(x) # x,y1,y2に対応する値のグラフを表示 plt.plot(x, y1, label='ReLU') plt.plot(x, y2, label='ReLU differential') plt.title("ReLU function and differential") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.legend() plt.grid() plt.show() |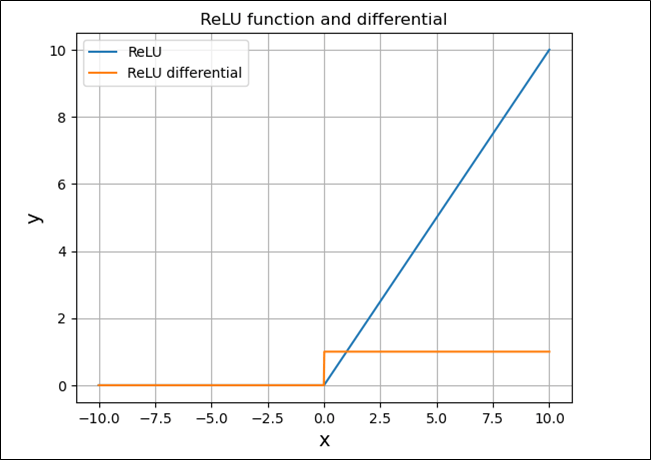
要点まとめ
- 以下の式で表現される関数をReLU関数といい、ディープラーニングの活性化関数の1つとして利用される。
\[
\begin{eqnarray}
f(x) = \left\{ \begin{array}{l} 0 （x＜0の場合）\\ x （x≧0の場合）\end{array} \right.
\end{eqnarray}
\] - 「勾配消失問題」の発生を防ぐため、ニューラルネットワークの中間層の活性化関数に「ReLU関数」がよく使われる。
- ReLU関数を\(x\)について微分すると、以下のようになる。
\[
\begin{eqnarray}
f(x) = \left\{ \begin{array}{l} 0 （x＜0の場合）\\ 1 （x≧0の場合）\end{array} \right.
\end{eqnarray}
\]
