入力値を\(y=(y_1,y_2,\ldots,y_K)\)、正解値を\(t=(t_1,t_2,\ldots,t_K)\)とした場合、以下の式で表現される式を「交差エントロピー誤差」といい、ディープラーニングの損失(誤差)関数の1つとして利用される。
\[
\begin{eqnarray}
L=- \displaystyle \sum_{k=1}^{K}t_k\mathrm{log}y_k
\end{eqnarray}
\]
例えば、入力値 \(y=(0.2,0.5,0.3)\)、正解値 \(t=(1,0,0)\)の場合、交差エントロピー誤差\(L=-(1 \times \mathrm{log}0.2 + 0 \times \mathrm{log}0.5 + 0 \times \mathrm{log}0.3)=-\mathrm{log}0.2≒1.6\) となる。
実際にこれをPythonプログラム上で計算した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | import numpy as np import sys # 底をネイピア数e(≒2.7)とする対数関数の値 def logq(y_list): # log0の計算ができないため、あらかめ # 微少な値(sys.float_info.epsilon)を加算しておく return np.log(y_list + sys.float_info.epsilon) # t_list * np.log(y_list)の値 def p_logq(t_list, y_list): return (t_list * logq(y_list)) # 交差エントロピー誤差の値 def cross_entropy(t_list, y_list): return -np.sum(p_logq(t_list, y_list)) # 検証用データ t_list = np.array([1, 0, 0]) y_list = np.array([0.2, 0.5, 0.3]) print("*** 引数のリスト t_list ***") print(t_list) print() print("*** 引数のリスト y_list ***") print(y_list) print() # 小数点以下16桁まで＋指数表記しない形式に設定 np.set_printoptions(precision=16, suppress=True) print("*** 底をネイピア数eとする対数関数の値 ***") print(logq(y_list)) print() print("*** t_list * np.log(y_list)の計算結果 ***") print(p_logq(t_list, y_list)) print() print("*** 交差エントロピー誤差の値 ***") print('{:.20f}'.format(cross_entropy(t_list, y_list))) |
また、上記サンプルプログラムで、y_list = np.array([0.8, 0.1, 0.1]) に変更した場合の計算結果は以下の通りで、先ほどより交差エントロピー誤差の値が小さくなっていることが確認できる。
さらに、上記サンプルプログラムで、y_list = np.array([1.0, 0.0, 0.0]) に変更した場合の計算結果は以下の通りで、交差エントロピー誤差の値が0に近づいていることが確認できる。
また、交差エントロピー誤差は下図のように、ディープラーニングで、活性化関数にソフトマックス関数を利用した場合の損失(誤差)関数として利用されることが多い。
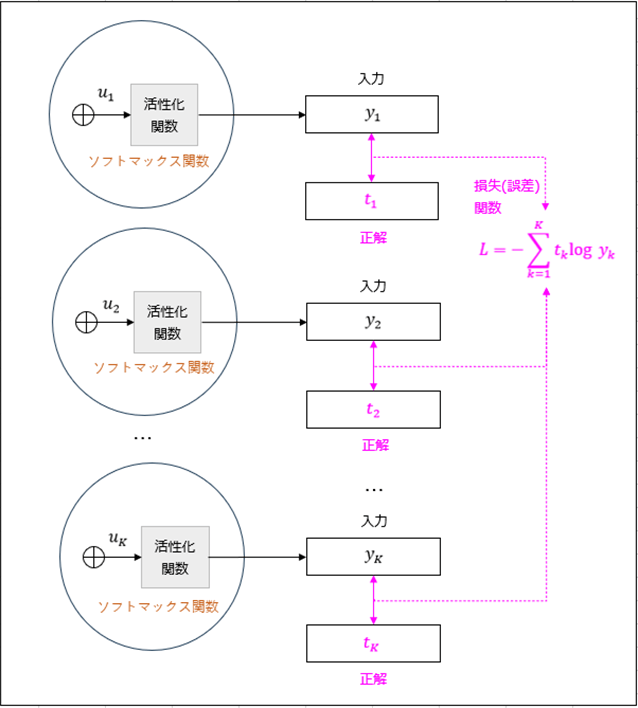
上記の場合の\(\displaystyle \frac{\partial L}{\partial u_k}\) を計算すると、以下のようになる。
\[
\begin{eqnarray}
\displaystyle \frac{\partial L}{\partial u_k} &=& \frac{\partial}{\partial u_k} \left( – \displaystyle \sum_{k=1}^{K}t_k\mathrm{log}y_k \right)
= \frac{\partial}{\partial u_k} \left( – \displaystyle \sum_{k=1}^{K}t_k\mathrm{log} \displaystyle \frac{e^{u_k}}{ \displaystyle \sum_{k=1}^{K}e^{u_k}} \right) \\
&=& \displaystyle \frac{\partial}{\partial u_k} \left( – \displaystyle \sum_{k=1}^{K}t_k \left( \mathrm{log}e^{u_k} – \mathrm{log}{ \displaystyle \sum_{k=1}^{K}e^{u_k}} \right) \right) \\
&=& \displaystyle \frac{\partial}{\partial u_k} \left( – \displaystyle \sum_{k=1}^{K}t_k \mathrm{log}e^{u_k} + \displaystyle \sum_{k=1}^{K}t_k \left( \mathrm{log}{ \displaystyle \sum_{k=1}^{K}e^{u_k}} \right) \right)
\end{eqnarray}
\]
ここで、\(\mathrm{log}e^{u_k}=u_k\)、かつ、\(\displaystyle \sum_{k=1}^{K}t_k=1\)なので、
\[
\begin{eqnarray}
\displaystyle \frac{\partial L}{\partial u_k} &=& \frac{\partial}{\partial u_k} \left( – \displaystyle \sum_{k=1}^{K}t_ku_k + \mathrm{log}{ \displaystyle \sum_{k=1}^{K}e^{u_k}} \right) \\
&=& – \displaystyle \frac{\partial}{\partial u_k} \sum_{k=1}^{K}t_ku_k + \frac{\partial}{\partial u_k} \mathrm{log}{ \displaystyle \sum_{k=1}^{K}e^{u_k}} \\
&=& -t_k + y_k = y_k – t_k
\end{eqnarray}
\]
なお、上記計算過程には、以下の式を利用している。
\[
\begin{eqnarray}
\displaystyle \frac{\partial}{\partial u_k} \sum_{k=1}^{K}t_ku_k &=& \frac{\partial}{\partial u_k} (t_1u_1 + t_2u_2 + \ldots + t_ku_k + \ldots + t_Ku_K) \\
&=& 0 + 0 + \ldots + t_k + \ldots + 0 = t_k \\
\frac{\partial}{\partial u_k} \mathrm{log}{ \displaystyle \sum_{k=1}^{K}e^{u_k}} &=& \displaystyle \frac{1}{\displaystyle \sum_{k=1}^{K}e^{u_k}} \frac{\partial}{\partial u_k}e^{u_k}
= \frac{e^{u_k}}{\displaystyle \sum_{k=1}^{K}e^{u_k}} = y_k
\end{eqnarray}
\]
以上より、\(\displaystyle \frac{\partial L}{\partial u_k} = y_k – t_k\)となる。
要点まとめ
- 以下の式で表現される式を「交差エントロピー誤差」という。
\[
\begin{eqnarray}
L=- \displaystyle \sum_{k=1}^{K}t_k\mathrm{log}y_k
\end{eqnarray}
\] - 交差エントロピー誤差は、ディープラーニングで、活性化関数にソフトマックス関数を利用した場合の損失(誤差)関数として利用される。
