統計

2変数の相関の強さを示す共分散や相関係数を計算してみた

 

2変数の関係は、散布図によって視覚的に表現できる。また、2変数の相関の強さを示す指標に「共分散」や「相関係数」がある。

今回は、2変数の関係を散布図で表現し、共分散・相関係数を算出してみたので、そのサンプルプログラムを共有する。

なお、共分散・相関係数については、以下のサイトを参照のこと。
https://hiraocafe.com/note/cov-r.html

前提条件

下記記事のAnacondaをインストールしJupyter Notebookを利用できること

Python開発用のAnacondaをインストールしJupyter Notebookを利用してみた今回は、Pythonを勉強してみたいと思い、Python開発環境を構築してみたので、その手順を共有する。 Python開発用として...

散布図の描画

入力データ\(x\),\(y\)の値(全\(20\)個)を読み込み、散布図として表示すると、以下のようになる。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]

# 入力データを散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
plt.show()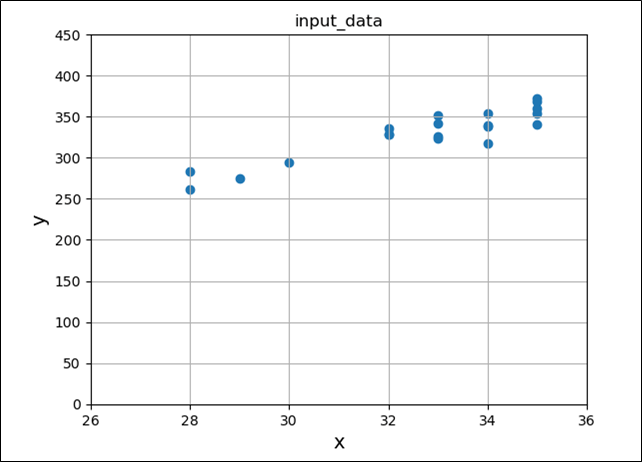
入力データの描画_実行結果

共分散の計算

データ\((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\)における(標本)共分散\(s_{xy}\)は、\(x_1\)～\(x_n\)の平均を\(\bar{x}\)、\(y_1\)～\(y_n\)の平均を\(\bar{y}\)とすると、 \(s_{xy}=\displaystyle \frac{1}{n}\sum_{i=1}^{n}\left(x_i – \bar{x}\right)\left(y_i – \bar{y}\right) \) と定義される。

また、(不偏)共分散は、(標本)共分散の式において\(n\)を\(n-1\)に置き換え、\(s_{xy}=\displaystyle \frac{1}{n-1}\sum_{i=1}^{n}\left(x_i – \bar{x}\right)\left(y_i – \bar{y}\right) \) と定義される。

入力データ\(x\),\(y\)の値(全\(20\)個)を読み込み、共分散を計算すると、以下のようになる。

import numpy as np

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]

# xの平均、yの平均の計算
input_x_ave = np.mean(input_data_x)
input_y_ave = np.mean(input_data_y)
print("*** 平均の計算 ***")
print("xの平均 : " + str(input_x_ave))
print("yの平均 : " + str(input_y_ave))
print()

# 共分散の計算
input_s_xy = 0
input_data_len = input_data_x.size
for i in range(input_data_len):
    input_s_xy += (input_data_x[i] - input_x_ave) * (input_data_y[i] - input_y_ave)
print("*** 共分散の計算(手動) ***")
print("(標本)共分散s_xy : " + str(input_s_xy / input_data_len))
print("(不偏)共分散s_xy : " + str(input_s_xy / (input_data_len - 1)))
print()
print("*** 共分散の計算(共分散行列) ***")
print("(標本)共分散行列")
print(np.cov(input_data_x, input_data_y, bias=True))
print("(標本)共分散s_xy : " + str(np.cov(input_data_x, input_data_y, bias=True)[0][1]))
print()
print("(不偏)共分散行列")
print(np.cov(input_data_x, input_data_y))
print("(不偏)共分散s_xy : " + str(np.cov(input_data_x, input_data_y)[0][1]))
共分散の計算



「DroidKit」はAndroid端末のデータ復元や画面ロック解除等が行える便利なツールだった「DroidKit」は、画面ロック解除、FRPバイパス、データ復元、システム修復、および4つのより効果的なツールを含んでいて、ほぼすべて...

相関係数の計算

共分散により、\(2\)変数の関係を数値で表現できたが、\(2\)変数の単位が違うため、異なるデータ間の相関の強さを比較できない。

データ\((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\)における相関係数\(r_{xy}\)は、\(x_1\)～\(x_n\)の平均を\(\bar{x}\)、\(y_1\)～\(y_n\)の平均を\(\bar{y}\)、\(x_1\)～\(x_n\)の標準偏差を\(s_x\)、\(y_1\)～\(y_n\)の標準偏差を\(s_y\)、(標本)共分散を\(s_{xy}\)とすると、 \(r_{xy}=\displaystyle \frac{s_{xy}}{s_xs_y}= \frac{1}{n}\sum_{i=1}^{n}\frac{\left(x_i – \bar{x}\right)}{s_x}\frac{\left(y_i – \bar{y}\right)}{s_y} \) と定義される。

入力データ\(x\),\(y\)の値(全\(20\)個)を読み込み、相関係数を計算すると、以下のようになる。

import numpy as np

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]

# xの平均、xの標準偏差、yの平均、yの標準偏差の計算
input_x_ave = np.mean(input_data_x)
input_x_std = np.std(input_data_x)
input_y_ave = np.mean(input_data_y)
input_y_std = np.std(input_data_y)
print("*** 平均・標準偏差の計算 ***")
print("xの平均 : " + str(input_x_ave))
print("xの標準偏差 : " + str(input_x_std))
print("yの平均 : " + str(input_y_ave))
print("yの標準偏差 : " + str(input_y_std))
print()

# 相関係数の計算
input_r_xy = 0
input_data_len = input_data_x.size
for i in range(input_data_len):
    input_r_xy += (input_data_x[i] - input_x_ave) / input_x_std \
                * (input_data_y[i] - input_y_ave) / input_y_std
print("*** 相関係数の計算(手動) ***")
print("相関係数r_xy : " + str(input_r_xy / input_data_len))
print()
print("*** 相関係数の計算(相関係数行列) ***")
print(np.corrcoef(input_data_x, input_data_y))
print("相関係数r_xy : " + str(np.corrcoef(input_data_x, input_data_y)[0][1]))
相関係数の計算

なお、相関係数\(r_{xy}\)は\(-1 ≦ r_{xy} ≦ 1\)の範囲内になり、\(r_{xy}\)が\(1\)に近いほど正の相関があり、\(r_{xy}\)が\(-1\)に近いほど負の相関がある。

そのイメージは、以下のサイトを参照のこと。
https://yasabi.co.jp/soukan-keisuu/

要点まとめ

  • 2変数の関係は、散布図によって視覚的に表現できる。また、2変数の相関の強さを示す指標に「共分散」や「相関係数」がある。
  • 相関係数\(r_{xy}\)は\(-1 ≦ r_{xy} ≦ 1\)の範囲内になり、\(r_{xy}\)が\(1\)に近いほど正の相関があり、\(r_{xy}\)が\(-1\)に近いほど負の相関がある。
RELATED POST