第3の変数の影響をなくした状態で、2変数間がどのように相関するか表す指標のことを、偏相関係数という。
今回は、Pingouinパッケージのpcorr関数を利用して、偏相関係数を算出してみたので、そのサンプルプログラムを共有する。
なお、偏相関係数については、以下のサイトを参照のこと。
https://best-biostatistics.com/correlation_regression/hen-soukan.html
前提条件
下記記事のAnacondaをインストールしJupyter Notebookを利用できること

pingouinパッケージのインストール
Pythonで偏相関係数を計算するライブラリを利用するには、Anacondaでpingouinパッケージを使えるようにする必要がある。その手順は、以下の通り。
1) Windowsのスタートメニューから「Anaconda Prompt」を選択する。
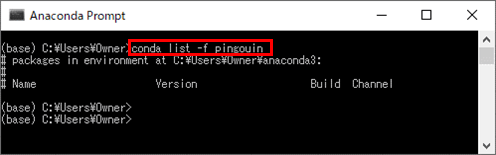
2) 以下のように、「conda list -f pingouin」コマンドを実行し、Anacondaにpingouinパッケージが含まれていないことを確認する。
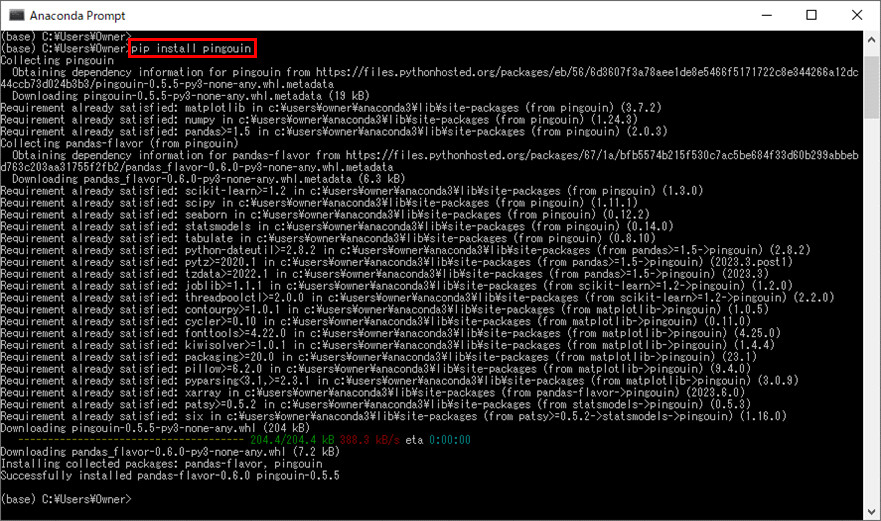
3)「pip install pingouin」コマンドを実行し、pingouinパッケージをインストールする。
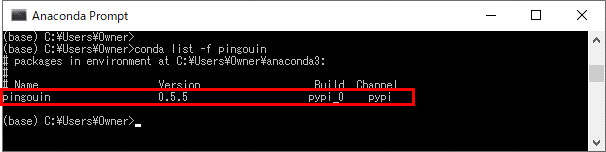
4)「conda list -f pingouin」コマンドを再度実行し、Anacondaにpingouinパッケージがインストールされたことを確認する。

偏相関係数の計算
入力データ\((x_1, y_1, z_1), (x_2, y_2, z_2), \ldots, (x_n, y_n, z_n)\)において、\(x\)と\(y\)の相関係数を\(r_{xy}\)、\(y\)と\(z\)の相関係数を\(r_{yz}\)、\(z\)と\(x\)の相関係数を\(r_{zx}\)とすると、\(z\)の影響を除いた\(x\)と\(y\)の偏相関係数\(r_{xy・z}\)は、\(r_{xy・z}=\displaystyle \frac{r_{xy}-r_{yz}r_{zx}}{\sqrt{1 – {r_{yz}}^2}\sqrt{1 – {r_{zx}}^2}}\)と定義される。
入力データ\(x\),\(y\),\(z\)の値(全\(20\)個)を読み込み、偏相関係数を計算すると、以下のようになる。
import numpy as np
import pandas as pd
import pingouin as pg
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# z座標を追加
input_data_z = np.array([3, 4, 4, 5, 5, 4, 4, 2, 1, 3, 2, 1, 3, 4, 3, 5, 3, 2, 4, 5])
# 相関係数
r_xy = np.corrcoef(input_data_x, input_data_y)[0][1]
r_yz = np.corrcoef(input_data_y, input_data_z)[0][1]
r_zx = np.corrcoef(input_data_z, input_data_x)[0][1]
print("*** 相関係数の計算(相関係数行列) ***")
print("相関係数r_xy : " + str(r_xy))
print("相関係数r_yz : " + str(r_yz))
print("相関係数r_zx : " + str(r_zx))
print()
# 偏相関係数
r_xy_z = (r_xy - r_yz * r_zx)/(np.sqrt(1 - r_yz**2) * np.sqrt(1 - r_zx**2))
r_yz_x = (r_yz - r_zx * r_xy)/(np.sqrt(1 - r_zx**2) * np.sqrt(1 - r_xy**2))
r_zx_y = (r_zx - r_xy * r_yz)/(np.sqrt(1 - r_xy**2) * np.sqrt(1 - r_yz**2))
print("*** 偏相関係数の計算(手動) ***")
print("偏相関係数r_xy_z : " + str(r_xy_z))
print("偏相関係数r_yz_x : " + str(r_yz_x))
print("偏相関係数r_zx_y : " + str(r_zx_y))
print()
print("*** 偏相関係数の計算(Pingouinパッケージのpcorr関数を利用) ***")
df = pd.DataFrame({"x":input_data_x,"y":input_data_y,"z":input_data_z})
print(pg.pcorr(df))
print("偏相関係数r_xy_z : " + str(pg.pcorr(df)["x"]["y"]))
print("偏相関係数r_yz_x : " + str(pg.pcorr(df)["y"]["z"]))
print("偏相関係数r_zx_y : " + str(pg.pcorr(df)["z"]["x"]))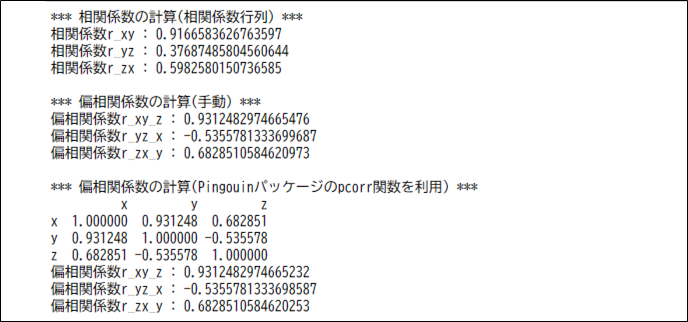
要点まとめ
- 第3の変数の影響をなくした状態で2変数間がどのように相関するか表す指標のことを、偏相関係数という。
- 偏相関係数は、Pingouinパッケージのpcorr関数を利用して計算できる。





