互いに独立な\(n\)回のベルヌーイ試行(=コインの裏表のように、何かを行ったときに起こる結果が\(2\)つしかない試行)を行うときに、初めて成功するまでの試行回数\(X\)が従う確率分布を幾何分布といい、\(k\)回目で初めて成功する確率は、以下の式で表せる。
\[
\begin{eqnarray}
P(X=k)=\left(1-p\right)^{k-1}p (k=1,2,3,\cdots)
\end{eqnarray}
\]
例えば、サイコロを投げて\(1\)または\(2\)の目が出る場合の試行結果を\(1\), それ以外の試行結果を\(0\)とした場合、\(p=\displaystyle \frac{1}{3}\)となるため、表形式でまとめると以下のようになる。
| \(k\) | 確率 |
|---|---|
| \(1\) | \(P(X=1)=\displaystyle \left(1-\frac{1}{3}\right)^{1-1} \times \frac{1}{3}=\left(\frac{2}{3}\right)^0 \times \frac{1}{3}=\frac{1}{3}≒0.3333 \) |
| \(2\) | \(P(X=2)=\displaystyle \left(1-\frac{1}{3}\right)^{2-1} \times \frac{1}{3}=\left(\frac{2}{3}\right)^1 \times \frac{1}{3}=\frac{2}{3} \times \frac{1}{3}=\frac{2}{9}≒0.2222 \) |
| \(3\) | \(P(X=3)=\displaystyle \left(1-\frac{1}{3}\right)^{3-1} \times \frac{1}{3}=\left(\frac{2}{3}\right)^2 \times \frac{1}{3}=\frac{4}{9} \times \frac{1}{3}=\frac{4}{27}≒0.1481 \) |
| \(4\) | \(P(X=4)=\displaystyle \left(1-\frac{1}{3}\right)^{4-1} \times \frac{1}{3}=\left(\frac{2}{3}\right)^3 \times \frac{1}{3}=\frac{8}{27} \times \frac{1}{3}=\frac{8}{81}≒0.0988 \) |
| \(5\) | \(P(X=5)=\displaystyle \left(1-\frac{1}{3}\right)^{5-1} \times \frac{1}{3}=\left(\frac{2}{3}\right)^4 \times \frac{1}{3}=\frac{16}{81} \times \frac{1}{3}=\frac{16}{243}≒0.0658 \) |
また、この確率を計算しグラフにまとめた場合の、ソースコードと実行結果は、以下のようになる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 幾何分布の計算 def geometric(k, p): return (1-p)**(k-1) * p # 幾何分布でp=1/3の場合の確率をそれぞれ計算 p = 1/3 p_list = list() for num in range(1, 11): p_list.append(geometric(num, p)) print("*** 幾何分布でp=1/3の場合の確率をそれぞれ計算した結果 ***") print("k=1の確率 = " + str(p_list[0])) print("k=2の確率 = " + str(p_list[1])) print("k=3の確率 = " + str(p_list[2])) print("k=4の確率 = " + str(p_list[3])) print("k=5の確率 = " + str(p_list[4])) print("k=6の確率 = " + str(p_list[5])) print("k=7の確率 = " + str(p_list[6])) print("k=8の確率 = " + str(p_list[7])) print("k=9の確率 = " + str(p_list[8])) print("k=10の確率 = " + str(p_list[9])) # 幾何分布でp=1/3の場合の確率を棒グラフで描画 k_list_array = np.arange(1, 11) p_list_array = np.array(p_list) plt.bar(k_list_array, p_list_array) plt.title("geometric graph") plt.xlabel("k", size=14) plt.ylabel("p", size=14) plt.show() |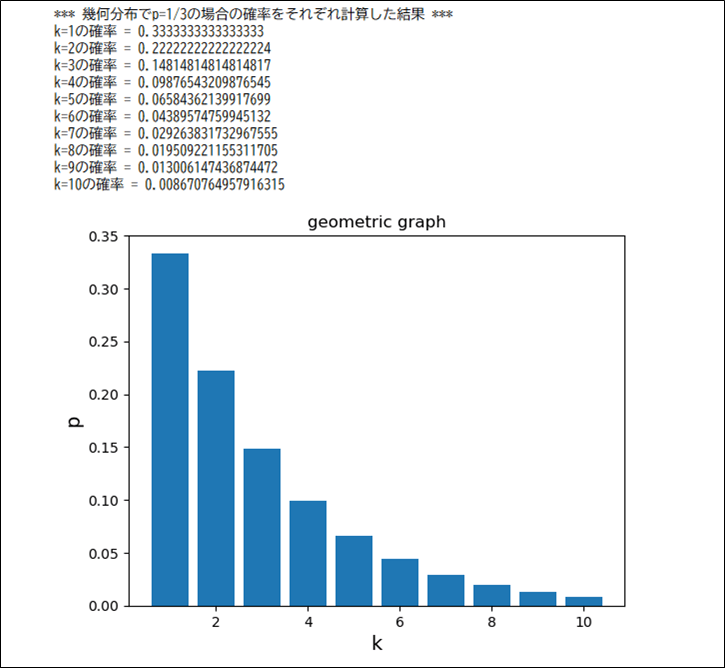
さらに、幾何分布の期待値\(E(X)\)と分散\(V(X)\)を計算する際、以下の無限等比級数の公式を利用する。
上記公式で、\(-1＜r＜1\)かつ\(a=1\)とすると、\(\displaystyle \sum_{k=1}^{\infty}r^{k-1}=1+r+r^2+\cdots=\frac{1}{1-r}\)となる。
また、この公式を利用して、幾何分布の期待値\(E(X)\)は、以下のように計算できる。
\[
\begin{eqnarray}
E(X) &=& p + 2(1-p)p + 3(1-p)^2p + 4(1-p)^3p + \cdots \\
上式で、q &=& 1-pと置き換えると、\\
E(X) &=& p + 2qp + 3q^2p + 4q^3p + \cdots ･･･① \\
qE(X) &=& qp + 2q^2p + 3q^3p + \cdots ･･･② \\
①-② &=& (1-q)E(X) = p + qp + q^2p + q^3p + \cdots \\
pE(X) &=& p(1 + q + q^2 + q^3 + \cdots ) \\
E(X) &=& 1 + q + q^2 + q^3 + \cdots = \displaystyle \frac{1}{1-q} = \frac{1}{p}
\end{eqnarray}
\]
さらに、幾何分布の分散\(V(X)\)は、以下のように計算できる。
\[
\begin{eqnarray}
V(X) &=& E(X^2) – {E(X)}^2 \\
E(X^2) &=& p + 2^2(1-p)p + 3^2(1-p)^2p + 4^2(1-p)^3p + \cdots \\
上式で、q &=& 1-pと置き換えると、\\
E(X^2) &=& p + 2^2qp + 3^2q^2p + 4^2q^3p + \cdots ･･･① \\
qE(X^2) &=& qp + 2^2q^2p + 3^2q^3p + \cdots ･･･② \\
①-② &=& (1-q)E(X^2) = p +3qp + 5q^2p + 7q^3p + \cdots \\
pE(X^2) &=& p(1 + 3q + 5q^2 + 7q^3 + \cdots) \\
E(X^2) &=& 1 + 3q + 5q^2 + 7q^3 + \cdots ･･･③ \\
qE(X^2) &=& q + 3q^2 + 5q^3 + \cdots ･･･④ \\
③-④ &=& (1-q)E(X^2) = 1 + 2q + 2q^2 + 2q^3 + \cdots = 1 + 2q(1 + q + q^2 + \cdots) \\
pE(X^2) &=& 1 + 2q \times \displaystyle \frac{1}{1-q} = 1 + 2q \times \displaystyle \frac{1}{p} = 1 + \frac{2q}{p} \\
E(X^2) &=& \displaystyle \frac{1}{p} + \frac{2q}{p^2} = \frac{p+2q}{p^2} \\
V(X) &=& E(X^2) – {E(X)}^2 = \displaystyle \frac{p+2q}{p^2} – \left(\frac{1}{p}\right)^2 = \frac{p+2q}{p^2} – \frac{1}{p^2} = \frac{p+2q-1}{p^2} \\
&=& \displaystyle \frac{2q-1+p}{p^2} = \frac{2q-(1-p)}{p^2} = \frac{2q-q}{p^2} = \frac{q}{p^2} = \frac{1-p}{p^2}
\end{eqnarray}
\]
なお、上記で利用している期待値と分散の公式については、以下のサイトを参照のこと。
https://toketarou.com/expectation/
要点まとめ
- \(n\)回のベルヌーイ試行を行うときに初めて成功するまでの試行回数\(X\)が従う確率分布を、幾何分布という。
- \(n\)回のベルヌーイ試行を行うときに\(k\)回目で初めて成功する確率は、\(\left(1-p\right)^{k-1}p\)で表せる。
- 幾何分布において、期待値\(E(X)=\displaystyle \frac{1}{p}\)、分散\(V(X)=\displaystyle \frac{1-p}{p^2}\)となる。
