ベルヌーイ分布のグラフを描画し期待値・分散を計算してみた

コインの裏表のように、何かを行ったときに起こる結果が\(2\)つしかない試行をベルヌーイ試行といい、この試行の結果を\(0\)と\(1\)で表した分布をベルヌーイ分布という。

例えば、サイコロを\(1\)回投げて\(1\)または\(2\)の目が出る場合の試行結果を\(1\), それ以外の試行結果を\(0\)とした場合の確率を表形式でまとめると、以下のようになる。

また、この分布をグラフにまとめた場合の、ソースコードと実行結果は、以下のようになる。

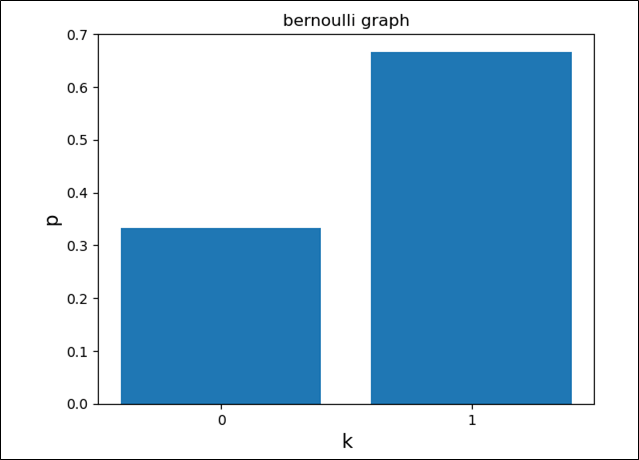
これを一般化し、試行結果が\(1\)となる確率を\(p\)とした場合の確率を表形式でまとめると、以下のようになる。

「EaseUS Partition Master」はパーティション分割・結合・作成・サイズ変更等を直感的に行える便利ツールだったハードディスクの記憶領域を論理的に分割し、分割された個々の領域のことを、パーティションといいます。 例えば、以下の図の場合、C/D...

また、試行結果が\(1\)となる確率を\(p\)とした場合のベルヌーイ分布について、期待値\(E(X)\)と分散\(V(X)\)を計算した結果は、以下の通り。
\[
\begin{eqnarray}
E(X) &=& \displaystyle \sum_{k=1}^{n}p_kx_k = (1-p) \times 0 + p \times 1 = 0+p = p \\
V(X) &=& \displaystyle \sum_{k=1}^{n}p_k \left\{x_k-E(X) \right\}^2 = E(X^2) – \left\{E(X)\right\}^2 = \sum_{k=1}^{n}p_kx_k^2 – p^2 \\
&=& \left\{(1-p) \times 0^2 + p \times 1^2\right\} – p^2 =\left\{0 + p\right\} – p^2 = p – p^2 = p(1-p)
\end{eqnarray}
\]

以上より、試行結果が\(1\)となる確率を\(p\)とした場合のベルヌーイ分布について、期待値\(E(X)=p\)、分散\(V(X)=p(1-p)\)となる。

なお、上記で利用している期待値と分散の公式については、以下のサイトを参照のこと。
https://toketarou.com/expectation/

例えば、サイコロを\(1\)回投げて\(1\)または\(2\)の目が出る場合の試行結果を\(1\), それ以外の試行結果を\(0\)とした場合の期待値\(E(X)\)と分散\(V(X)\)を計算した結果は、以下の通り。
\[
\begin{eqnarray}
E(X) &=& p = \displaystyle \frac{1}{3} ≒ 0.333 \\
V(X) &=& p(1-p) = \displaystyle \frac{1}{3} \times \left(1-\frac{1}{3}\right) = \displaystyle \frac{1}{3} \times \frac{2}{3} = \frac{2}{9} ≒ 0.222
\end{eqnarray}
\]

要点まとめ

• コインの裏表のように、何かを行ったときに起こる結果が\(2\)つしかない試行のことをベルヌーイ試行といい、この試行の結果を\(0\)と\(1\)で表した分布をベルヌーイ分布という。
• ベルヌーイ分布の試行結果が\(1\)となる確率を\(p\)とした場合、期待値\(E(X)=p\)、
  分散\(V(X)=p(1-p)\)となる。