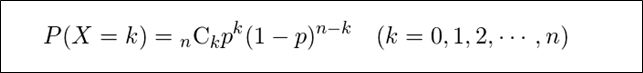二項分布の計算を行いグラフを描いてみた｜ITエンジニアとして経験・学習したこと

(通常の)コインを何回か投げて表が出る確率を考える。例えば、(通常の)コインを5回投げて表が2回出る確率は、以下のように計算することができる。

\[
\begin{eqnarray}
P(X=2) &=& {}_5 \mathrm{ C }_2(\frac{1}{2})^2(1 – \frac{1}{2})^{(5-2)} \\
&=& \frac{{}_5 \mathrm{ P }_2}{2!}(\frac{1}{2})^2(\frac{1}{2})^3 = \frac{(5 \times 4)}{(2 \times 1)}(\frac{1}{2})^5 \\
&=& 10 \times \frac{1}{32} = \frac{10}{32} = 0.3125 \\
\end{eqnarray}
\]

これを一般化し、\(n\)回のベルヌーイ試行(=コインの裏表のように、何かを行ったときに起こる結果が2つしかない試行)を行うときにちょうど\(k\)回成功する確率は、以下の式で表せる。

出所：統計WEB_二項分布

実際に、(通常の)コインを5回投げて表が出る確率を表形式でまとめると、以下のようになる。

表が出る回数	確率
\(0\)	\(\displaystyle {}_5 \mathrm{ C }_0(\frac{1}{2})^0(1 – \frac{1}{2})^{(5-0)} = \frac{1}{32} = 0.03125 \)
\(1\)	\(\displaystyle {}_5 \mathrm{ C }_1(\frac{1}{2})^1(1 – \frac{1}{2})^{(5-1)} = \frac{5}{32} = 0.15625 \)
\(2\)	\(\displaystyle {}_5 \mathrm{ C }_2(\frac{1}{2})^2(1 – \frac{1}{2})^{(5-2)} = \frac{10}{32} = 0.3125 \)
\(3\)	\(\displaystyle {}_5 \mathrm{ C }_3(\frac{1}{2})^3(1 – \frac{1}{2})^{(5-3)} = \frac{10}{32} = 0.3125 \)
\(4\)	\(\displaystyle {}_5 \mathrm{ C }_4(\frac{1}{2})^4(1 – \frac{1}{2})^{(5-4)} = \frac{5}{32} = 0.15625 \)
\(5\)	\(\displaystyle {}_5 \mathrm{ C }_5(\frac{1}{2})^5(1 – \frac{1}{2})^{(5-5)} = \frac{1}{32} = 0.03125 \)

また、コインを5回投げて表が出る確率を計算しグラフにまとめた場合の、ソースコードと実行結果は、以下のようになる。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# n!(=1*2*･･･*n、nの階乗)を計算
def factorial(n):
    ret = 1
    for num in range(1, n + 1):
        ret = ret * num
    return ret

# {}_n \mathrm{ P }_k(n個からk個を並べる組み合わせ)を計算
def permutation(n, k):
    ret = 1
    for num in range(n + 1- k, n + 1):
        ret = ret * num
    return ret

# {}_n \mathrm{ C }_k(n個からk個を取り出す組み合わせ)を計算
def combination(n, k):
    return permutation(n, k) / factorial(k)

# 二項分布(コインをn回投げて表がk回出る確率)の計算
def binomial(n, k):
    return combination(n, k) / 2 ** n

# コインを5回投げて表がk回出る確率をそれぞれ計算
p_list = list()
for num in range(0, 6):
    p_list.append(binomial(5, num))

print("*** コインを5回投げて表がk回出る確率をそれぞれ計算した結果 ***")
print("表が出る回数 0の確率 = " + str(p_list[0]))
print("表が出る回数 1の確率 = " + str(p_list[1]))
print("表が出る回数 2の確率 = " + str(p_list[2]))
print("表が出る回数 3の確率 = " + str(p_list[3]))
print("表が出る回数 4の確率 = " + str(p_list[4]))
print("表が出る回数 5の確率 = " + str(p_list[5]))

# コインを5回投げて表がk回出る確率を棒グラフで描画
k_list_array = np.array([0, 1, 2, 3, 4, 5])
p_list_array = np.array(p_list)
plt.bar(k_list_array, p_list_array)
plt.title("binomial graph")
plt.xlabel("k", size=14)
plt.ylabel("p", size=14)
plt.show()

%matplotlib inline

import numpy as np

import matplotlib.pyplot as plt

# n!(=1*2*･･･*n、nの階乗)を計算

def factorial(n):

ret = 1

for num in range(1, n + 1):

ret = ret * num

return ret

# {}_n \mathrm{ P }_k(n個からk個を並べる組み合わせ)を計算

def permutation(n, k):

ret = 1

for num in range(n + 1- k, n + 1):

ret = ret * num

return ret

# {}_n \mathrm{ C }_k(n個からk個を取り出す組み合わせ)を計算

def combination(n, k):

return permutation(n, k) / factorial(k)

# 二項分布(コインをn回投げて表がk回出る確率)の計算

def binomial(n, k):

return combination(n, k) / 2 ** n

# コインを5回投げて表がk回出る確率をそれぞれ計算

p_list = list()

for num in range(0, 6):

p_list.append(binomial(5, num))

print("*** コインを5回投げて表がk回出る確率をそれぞれ計算した結果 ***")

print("表が出る回数 0の確率 = " + str(p_list[0]))

print("表が出る回数 1の確率 = " + str(p_list[1]))

print("表が出る回数 2の確率 = " + str(p_list[2]))

print("表が出る回数 3の確率 = " + str(p_list[3]))

print("表が出る回数 4の確率 = " + str(p_list[4]))

print("表が出る回数 5の確率 = " + str(p_list[5]))

# コインを5回投げて表がk回出る確率を棒グラフで描画

k_list_array = np.array([0, 1, 2, 3, 4, 5])

p_list_array = np.array(p_list)

plt.bar(k_list_array, p_list_array)

plt.title("binomial graph")

plt.xlabel("k", size=14)

plt.ylabel("p", size=14)

plt.show()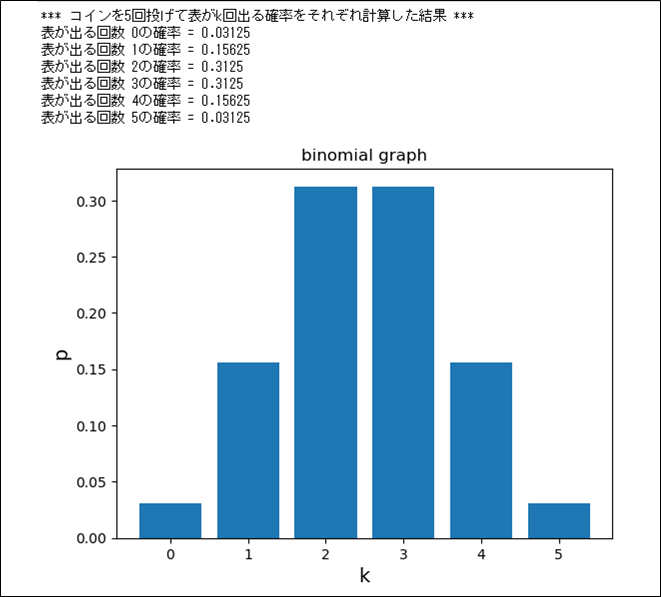

このように、起こりうることがらに割り当てている値(上記の例では、表が出る回数0～5)のことを確率変数といい、確率変数がとる値とその値をとる確率の対応の様子を確率分布という。また、\(n\)回のベルヌーイ試行を行うときにちょうど\(k\)回成功する場合の確率分布を、二項分布という。

同様に、コインを30回投げて表が出る確率を計算しグラフにまとめた場合の、ソースコードと実行結果は、以下のようになる。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# n!(=1*2*･･･*n、nの階乗)を計算
def factorial(n):
    ret = 1
    for num in range(1, n + 1):
        ret = ret * num
    return ret

# {}_n \mathrm{ P }_k(n個からk個を並べる組み合わせ)を計算
def permutation(n, k):
    ret = 1
    for num in range(n + 1- k, n + 1):
        ret = ret * num
    return ret

# {}_n \mathrm{ C }_k(n個からk個を取り出す組み合わせ)を計算
def combination(n, k):
    return permutation(n, k) / factorial(k)

# 二項分布(コインをn回投げて表がk回出る確率)の計算
def binomial(n, k):
    return combination(n, k) / 2 ** n

# コインを30回投げて表がk回出る確率をそれぞれ計算
p_list = list()
for num in range(0, 31):
    p_list.append(binomial(30, num))

# コインを30回投げて表がk回出る確率を棒グラフで描画
k_list_array = np.array(range(0, 31))
p_list_array = np.array(p_list)
plt.bar(k_list_array, p_list_array)
plt.title("binomial graph")
plt.xlabel("k", size=14)
plt.ylabel("p", size=14)
plt.show()

%matplotlib inline

import numpy as np

import matplotlib.pyplot as plt

# n!(=1*2*･･･*n、nの階乗)を計算

def factorial(n):

ret = 1

for num in range(1, n + 1):

ret = ret * num

return ret

# {}_n \mathrm{ P }_k(n個からk個を並べる組み合わせ)を計算

def permutation(n, k):

ret = 1

for num in range(n + 1- k, n + 1):

ret = ret * num

return ret

# {}_n \mathrm{ C }_k(n個からk個を取り出す組み合わせ)を計算

def combination(n, k):

return permutation(n, k) / factorial(k)

# 二項分布(コインをn回投げて表がk回出る確率)の計算

def binomial(n, k):

return combination(n, k) / 2 ** n

# コインを30回投げて表がk回出る確率をそれぞれ計算

p_list = list()

for num in range(0, 31):

p_list.append(binomial(30, num))

# コインを30回投げて表がk回出る確率を棒グラフで描画

k_list_array = np.array(range(0, 31))

p_list_array = np.array(p_list)

plt.bar(k_list_array, p_list_array)

plt.title("binomial graph")

plt.xlabel("k", size=14)

plt.ylabel("p", size=14)

plt.show()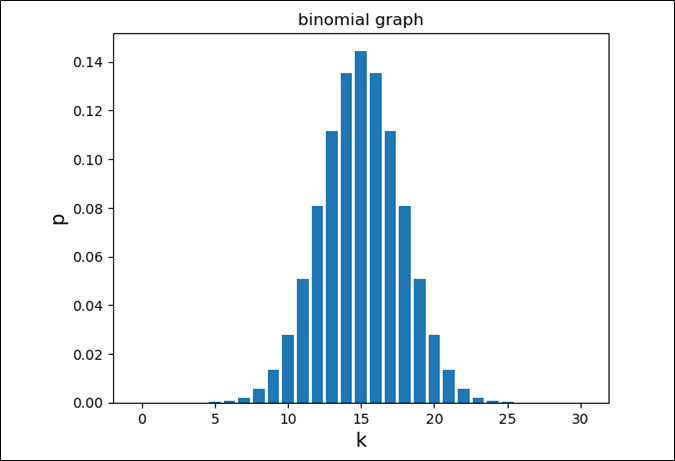

このグラフから、\(k=15\)付近が最も確率が高く、\(k=15\)から離れるに従い、確率が\(0\)に近づくことが確認できる。

なお、二項分布で\(n\)が十分大きい場合、確率の計算が難しくなるが、以下のポアソン分布に近似して計算することができる。

出所：統計WEB_ポアソン分布

ポアソン分布の証明については、例えば以下のサイトを参照のこと。
https://www.eeso.ges.kyoto-u.ac.jp/emm/materials/basic_stat/pisson

要点まとめ

コインの裏表のように、何かを行ったときに起こる結果が2つしかない試行を、ベルヌーイ試行という。
\(n\)回のベルヌーイ試行を行うときにちょうど\(k\)回成功する確率は、\( {}_n \mathrm{ C }_kp^k(1 – p)^{(n-k)} \)で表せる。
\(n\)回のベルヌーイ試行を行うときにちょうど\(k\)回成功する場合の確率分布を、二項分布という。
二項分布で\(n\)が十分大きい場合、確率の計算が難しくなるが、ポアソン分布に近似して計算することができる。