二項分布に従うある事象が起こる確率\(p\)が分からない状態で、\(5\)回中\(3\)回ある事象が起きた場合に、最も起こりうる確率を考える。
この場合の確率は、以下の式で表現できる。
\[
\begin{eqnarray}
L(p) = {}_5 \mathrm{ C }_3 p^3(1-p)^2 (0 ≦ p ≦ 1)
\end{eqnarray}
\]
このように、想定するパラメーターがある値をとる場合に、観測している事柄や事象が起こりうる確率を表現したものを尤度関数という。
なお、二項分布の公式やグラフについては、以下の記事を参照のこと。
先ほどの\(L(p) = {}_5 \mathrm{ C }_3 p^3(1-p)^2 \ (0 ≦ p ≦ 1)\)をグラフ化した結果は、以下のようになる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 二項分布に従う尤度関数の計算 # ある事象が5回中3回起きる確率をpとしている def likelihood_func(p): return 10 * p**3 * (1-p)**2 # 0～1までを100等分した値をpとする p = np.linspace(0, 1, 100) # ある事象が5回中3回起きる確率をpとした場合の # 尤度関数の計算結果をLとする L = likelihood_func(p) # p, Lの値の変化をグラフに表示 plt.plot(p, L) plt.title("likelihood function graph") plt.xlabel("p", size=14) plt.ylabel("L", size=14) plt.grid() plt.show() |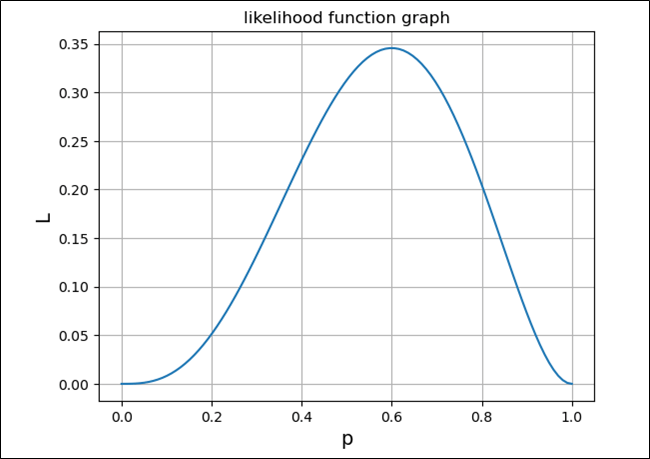
このように、\(p=0.6\)の場合に、尤度関数が最大になることが確認できる。これは、\(5\)回中\(3\)回ある事象が起こる確率を感覚的に計算した場合の、\(\displaystyle \frac{3}{5}=0.6\)と一致している。
また、尤度関数を計算する際、乗算を多く含むと計算しにくいため、尤度関数\(L\)に自然対数をとった対数尤度関数を利用する場合も多い。
先ほどの\(L(p) = {}_5 \mathrm{ C }_3 p^3(1-p)^2\)から、対数尤度関数を計算すると、以下のようになる。
\[
\begin{eqnarray}
logL(p) &=& log \{ {}_5 \mathrm{ C }_3 p^3(1-p)^2 \} \\
&=& log{}_5 \mathrm{ C }_3 + logp^3 + log(1-p)^2 \\
&=& log10 + 3logp + 2log(1-p)
\end{eqnarray}
\]
なお、上記計算を行うにあたって、対数関数の以下の公式を利用している。
\[
\begin{eqnarray}
logAB &=& logA + logB \\
logA^n &=& nlogA
\end{eqnarray}
\]
先ほどの\(logL(p) = log10 + 3logp + 2log(1-p) \ (0 ≦ p ≦ 1)\)をグラフ化した結果は、以下のようになる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 二項分布に従う対数尤度関数の計算 # ある事象が5回中3回起きる確率をpとしている def logarithm_likelihood_func(p): return np.log(10) + 3 * np.log(p) + 2 * np.log(1-p) # 0.001～0.999までを100等分した値をpとする # 0の自然対数(np.log(0))は未定義なので、 # 0の自然対数を含まない範囲で計算している p = np.linspace(0.001, 0.999, 100) # ある事象が5回中3回起きる確率をpとした場合の # 対数尤度関数の計算結果をlogLとする logL = logarithm_likelihood_func(p) # p, logLの値の変化をグラフに表示 plt.plot(p, logL) plt.title("logarithm likelihood function graph") plt.xlabel("p", size=14) plt.ylabel("logL", size=14) plt.grid() plt.show() # p=0.5～0.7の場合の、対数尤度関数の値をそれぞれ出力 print("*** p=0.5～0.7の場合の対数尤度関数の値 ***") print("p=0.5の場合 ： " + str(logarithm_likelihood_func(0.5))) print("p=0.55の場合： " + str(logarithm_likelihood_func(0.55))) print("p=0.6の場合 ： " + str(logarithm_likelihood_func(0.6))) print("p=0.65の場合： " + str(logarithm_likelihood_func(0.65))) print("p=0.7の場合 ： " + str(logarithm_likelihood_func(0.7))) |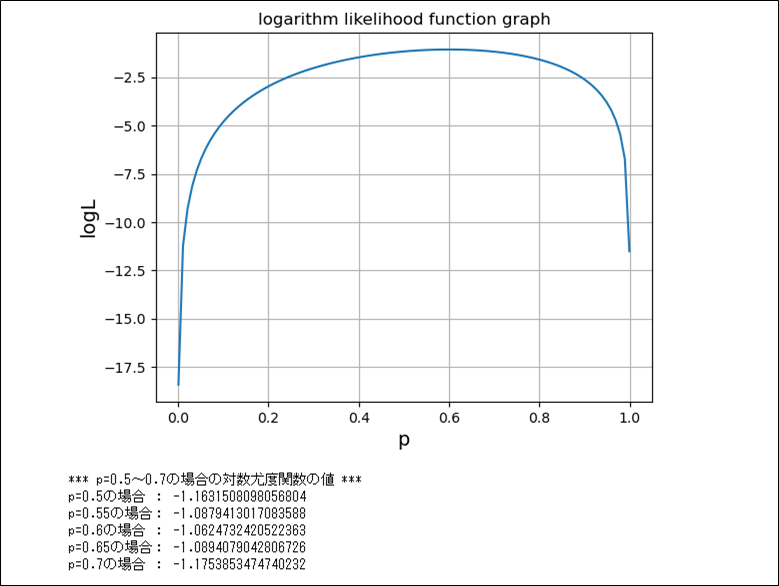
上記より、\(L(p)\)の大小関係と、\(logL(p)\)の大小関係が同じで、対数尤度関数が最大になるのも\(p=0.6\)の場合であることが確認できる。
さらに、対数尤度関数\(logL(p)\)が最大になる\(p\)は、\(logL(p)\)を\(p\)について微分して計算した傾きがゼロになる値となる。\(logL(p)\)を\(p\)について微分した計算結果は、以下のようになる。
\[
\begin{eqnarray}
logL(p) &=& log10 + 3logp + 2log(1-p) \\
\frac{d}{dp} \{logL(p)\} &=& \frac{d}{dp} \{log10 + 3logp + 2log(1-p)\} \\
&=& \frac{d}{dp} \{log10\} + \frac{d}{dp}\{3logp\} + \frac{d}{dp}\{2log(1-p)\} \\
&=& 0 + 3\frac{d}{dp}\{logp\} + 2\frac{d}{dp}\{log(1-p)\} \\
&=& \frac{3}{p} – \frac{2}{(1-p)}
\end{eqnarray}
\]
なお、上記計算を行うにあたって、以下の式を利用している。
\[
\begin{eqnarray}
\frac{d}{dp}\{logp\} &=& \frac{1}{p} \\
\frac{d}{dp}\{log(1-p)\} &=& \frac{1}{(1-p)} \times \frac{d}{dp}(1-p) = -\frac{1}{(1-p)}
\end{eqnarray}
\]
先ほどの二項分布に従う対数尤度関数のグラフに、微分した対数尤度関数のグラフを追加した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 二項分布に従う対数尤度関数の計算 # ある事象が5回中3回起きる確率をpとしている def log_likelihood_func(p): return np.log(10) + 3 * np.log(p) + 2 * np.log(1-p) # 二項分布に従う対数尤度関数の微分の計算 # ある事象が5回中3回起きる確率をpとしている def diff_log_likelihood_func(p): return 3 / p - 2 / (1-p) # 0.001～0.999までを100等分した値をp1とする p1 = np.linspace(0.001, 0.999, 100) # 0.2～0.9までを100等分した値をp2とする # 0.001～0.2, 0.9～0.999は対数尤度関数の微分値が # 大きくなるため、範囲外としている p2 = np.linspace(0.2, 0.9, 100) # ある事象が5回中3回起きる確率をxとした場合の # 対数尤度関数の計算結果をy1, その微分をy2とする logL1 = log_likelihood_func(p1) logL2 = diff_log_likelihood_func(p2) # p1, logL1, p2, logL2の値の変化をグラフに表示 plt.plot(p1, logL1, label="log_likelihood_func") plt.plot(p2, logL2, label="diff_log_likelihood_func") plt.title("logarithm likelihood function graph") plt.xlabel("p", size=14) plt.ylabel("logL", size=14) plt.legend() plt.grid() plt.show() |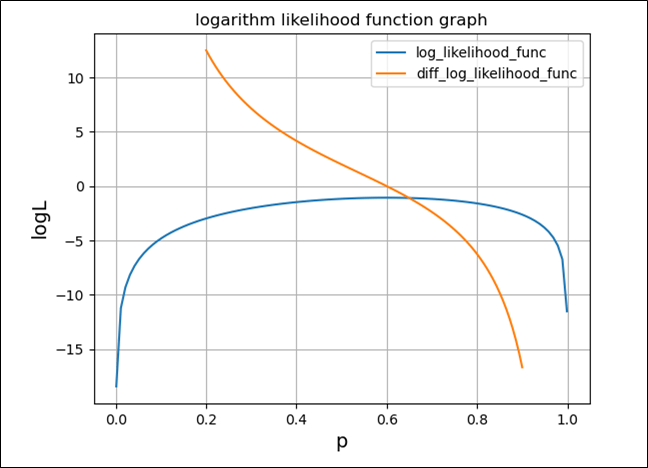
\(\displaystyle \frac{d}{dp} \{logL(p)\} = \frac{3}{p} – \frac{2}{(1-p)}\)が\(0\)になる\(p\)を計算した結果は以下の通りで、上記グラフと同様、\(p=0.6\)となる。
\[
\begin{eqnarray}
\frac{3}{p} – \frac{2}{(1-p)} &=& 0 \\
3(1-p)-2p &=& 0 \\
3-3p-2p &=& 0 \\
-5p &=& -3 \\
p &=& \frac{3}{5} = 0.6
\end{eqnarray}
\]
なお、上記\(p\)の値は、以下の記事に記載の最急降下法を用いて算出することもできる。
要点まとめ
- 想定するパラメーターがある値をとる場合に、観測している事柄や事象が起こりうる確率を表現したものを尤度関数という。
- 尤度関数を計算する際、乗算を多く含むと計算しにくいため、尤度関数\(L\)に自然対数をとった対数尤度関数を利用する場合も多い。
- 二項分布に従う対数尤度関数の最大値をとる確率\(p\)は、その微分が\(0\)になる値を計算することで求められる。
