ロジスティクス回帰分析の対数尤度関数を偏微分してみた

以下の記事で、ロジスティック回帰分析に従う、アヤメがvirginicaである確率$p$の計算式を算出してきた。

(分類を行う)ロジスティック回帰分析の相乗モデルから発生確率を計算してみた 代表的な機械学習フレームワークであるscikit-learnに、アヤメのデータセットが含まれているため、これを利用したアヤメの分類を...

上記記事で算出した確率$p$の計算式は、petal length (cm)を$\mathrm{pl}$、petal width (cm)を$\mathrm{pw}$と記載すると、以下の通り。
$$\begin{eqnarray} p &=& \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \\\\ p &:& アヤメが\mathrm{virginica}である確率 \\ B &:& 条件0（\mathrm{pl}＜5、かつ、\mathrm{pw}＜1.7）のオッズ \\ A_1 &:& （条件0に対する）条件1（\mathrm{pl}≧5）のオッズ比 \\ x_1 &:& （条件1に対する）0か1の値 \\ A_2 &:& （条件0に対する）条件2（\mathrm{pw}≧1.7）のオッズ比 \\ x_2 &:& （条件2に対する）0か1の値 \\ b &:& \log B \\ a_1 &:& \log A_1 \\ a_2 &:& \log A_2 \end{eqnarray}$$

今回は、算出した $p = \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }}$ の最適解となる$b$, $a_1$, $a_2$を算出するための対数尤度関数とその偏微分を算出してみたので、その結果を共有する。

例えば以下のデータの場合、先頭$51$～$55$行目のデータは全て$x_1=0$、$x_2=0$、$p=0$となり、先頭$101$～$105$行目のデータは全て、$x_1=1$、$x_2=1$、$p=1$となる。

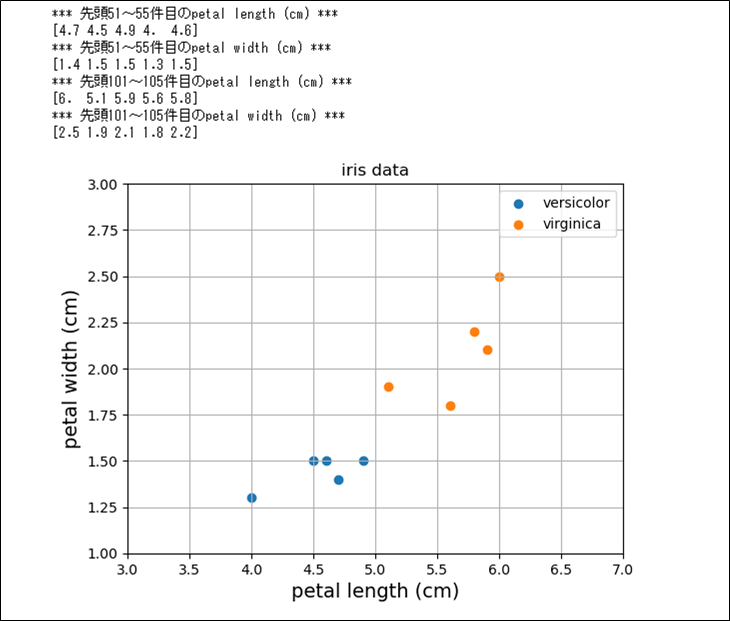
そのため、上記$10$データを利用して、尤度関数$L$を算出すると、以下のようになる。
$$\begin{eqnarray} L &=& (1-p)^5p^5 \\ &=& \left\{ 1-\displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \right\}^5 \left\{ \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \right\}^5 \\ &=& \left\{ 1-\displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1} \times 0 + {a_2} \times 0) \} }} \right\}^5 \left\{ \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1} \times 1 + {a_2} \times 1) \} }} \right\}^5 \end{eqnarray}$$

また、上記計算は煩雑になるため、尤度関数$L$に自然対数をとった対数尤度関数$\log L$を算出する。その結果は、以下の通り。
$$\begin{eqnarray} \log L &=& \log \{(1-p)^5p^5\} = \log (1-p)^5 + \log p^5 = 5 \log (1-p) + 5 \log p \\ &=& 5 \log \left\{ 1 – \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \right\} + 5 \log \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \\ &=& 5 \log \left\{ 1 – \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1} \times 0 + {a_2} \times 0) \} }} \right\} + 5 \log \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1} \times 1 + {a_2} \times 1) \} }} \end{eqnarray}$$

前述の$10$データを利用して、$L$, $\log L$を実際にグラフ化すると以下のようになり、それぞれ上に凸のグラフとなる。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# ロジスティクス回帰分析で、10回中5回結果が1になる
# 確率をpとした場合の尤度関数
def func_L(p):
    return (1-p)**5*p**5

# 0～1までを100等分した値をpとする
p = np.linspace(0, 1, 100)

# 尤度関数の計算結果をLとする
L = func_L(p)

# p, Lの値の変化をグラフに表示
plt.plot(p, L)
plt.title("likelihood function graph")
plt.xlabel("p", size=14)
plt.ylabel("L", size=14)
plt.grid()
plt.show()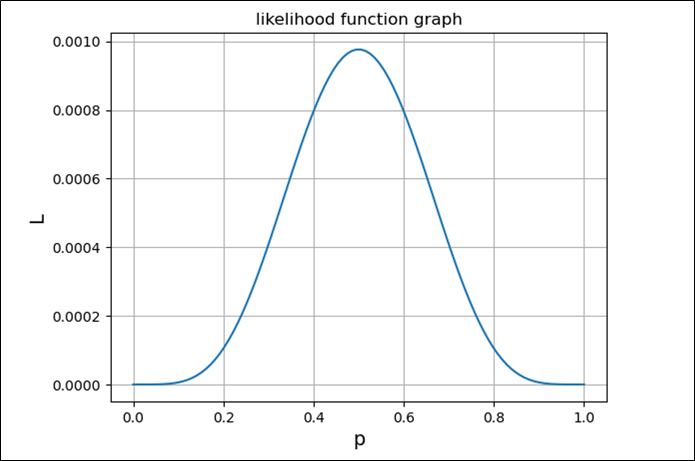

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# ロジスティクス回帰分析で、10回中5回結果が1になる
# 確率をpとした場合の対数尤度関数
def func_logL(p):
    return np.log((1-p)**5*p**5)

# 0.001～0.999までを100等分した値をpとする
# 0の自然対数(np.log(0))は未定義なので、
# 0の自然対数を含まない範囲で計算している
p = np.linspace(0.001, 0.999, 100)

# 対数尤度関数の計算結果をLとする
L = func_logL(p)

# p, Lの値の変化をグラフに表示
plt.plot(p, L)
plt.title("likelihood function graph")
plt.xlabel("p", size=14)
plt.ylabel("logL", size=14)
plt.grid()
plt.show()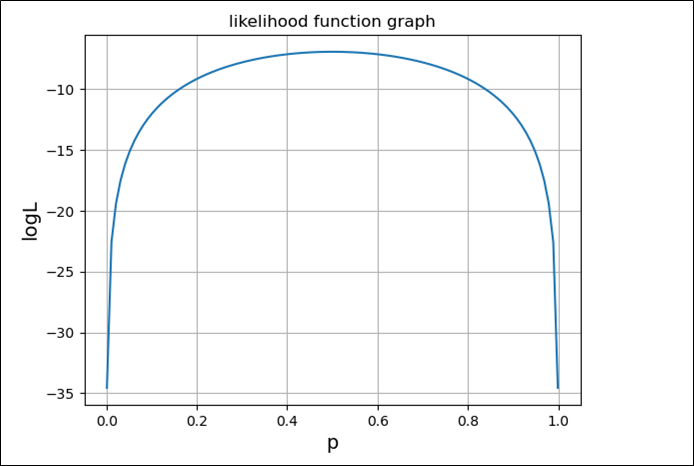

「EaseUS Todo Backup」は様々な形でバックアップ取得が行える便利ツールだったパソコン内のデータを、ファイル/パーティション/ディスク等の様々な単位でバックアップしたり、バックアップのスケジュール設定や暗号化設定も...

尤度関数$L$を一般化し、$n$回中$m$回が$p=1$、それ以外の$(n-m)$回が$p=0$とすると、以下のように表せる。
$$\begin{eqnarray} L &=& (1-p)^{(n-m)}p^m \\ &=& \left\{ 1-\displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \right\}^{(n-m)} \left\{ \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \right\}^m \end{eqnarray}$$

また、対数尤度関数$\log L$を一般化し、$n$回中$m$回が$p=1$、それ以外の$(n-m)$回が$p=0$とすると、以下のように表せる。
$$\begin{eqnarray} \log L &=& \log \{(1-p)^{(n-m)}p^m\} = \log (1-p)^{(n-m)} + \log p^m = (n-m) \log (1-p) + m \log p \\ &=& (n-m) \log \left\{ 1 – \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \right\} + m \log \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \end{eqnarray}$$

$x_1$, $x_2$, $p$が与えられた場合に、対数尤度関数$\log L$が最大になる$a_1$, $a_2$, $b$が最適解になる。
対数尤度関数$\log L$が最大になる時、$\displaystyle \frac{\partial}{\partial a_1} \log L = \displaystyle \frac{\partial}{\partial a_2} \log L = \displaystyle \frac{\partial}{\partial b} \log L = 0$となるため、$\log L$の$a_1$, $a_2$, $b$に関する偏微分を、それぞれ算出する。

$\displaystyle \frac{\partial}{\partial a_1} \log L\ = \frac{\partial}{\partial a_1} \left\{ (n-m) \log (1-p) + m \log p \right\}$となるため、まずは$\displaystyle \frac{\partial}{\partial a_1} \log (1-p)$, $\displaystyle \frac{\partial}{\partial a_1} \log p$をそれぞれ算出する。

$u = b + {a_1}{x_1} + {a_2}{x_2}$、$p = \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \}}} = \frac{1}{1 + \exp{(-u)}}$ と置くと、
$$\begin{eqnarray} \displaystyle \frac{\partial}{\partial a_1} \log (1-p) &=& \frac{\partial}{\partial p} \log (1-p) \frac{\partial p}{\partial u} \frac{1}{1 + \exp{(-u)}} \frac{\partial u}{\partial a_1}(b + {a_1}{x_1} + {a_2}{x_2}) \\ &=& \displaystyle \frac{1}{1-p} \frac{\partial}{\partial p}(1-p) \times p(1-p) \times {x_1} \\ &=& \frac{1}{1-p} \times (-1) \times p(1-p) \times {x_1} = -1 \times p \times {x_1} = -{x_1}p \\\\ \displaystyle \frac{\partial}{\partial a_1} \log p &=& \frac{\partial}{\partial p} \log p \frac{\partial p}{\partial u} \frac{1}{1 + \exp{(-u)}} \frac{\partial u}{\partial a_1}(b + {a_1}{x_1} + {a_2}{x_2}) \\ &=& \displaystyle \frac{1}{p} \times p(1-p) \times {x_1} = (1-p) \times {x_1} = {x_1}(1-p) \end{eqnarray}$$

上記計算では、合成関数の微分公式と、$\displaystyle \frac{ \mathrm{d}}{ \mathrm{d} x} \log x = \frac{1}{x}$になることと、標準シグモイド関数$f(x)=\displaystyle \frac{1}{1 + e^{-x}} = \frac{1}{1 + \exp{(-x)}}$を微分すると$f(x)(1 – f(x))$となることを利用している。

合成関数の微分公式については、以下のサイトを参照のこと。
https://manabitimes.jp/math/936

また、$\displaystyle \frac{ \mathrm{d}}{ \mathrm{d} x} \log x = \frac{1}{x}$については、以下のサイトを参照のこと。
https://atarimae.biz/archives/12831

さらに、標準シグモイド関数の微分については、以下のサイトを参照のこと。

標準シグモイド関数とその微分をグラフ化してみた $f(x)=\displaystyle \frac{1}{1 + e^{-ax}}　(a > 0)$で表現される関数をシグモイド...

そのため、$\displaystyle \frac{\partial}{\partial a_1} \log L$を計算すると、以下のようになる。
$$\begin{eqnarray} \displaystyle \frac{\partial}{\partial a_1} \log L &=& \frac{\partial}{\partial a_1} \left\{ (n-m) \log (1-p) + m \log p \right\} \\ &=& (n-m) \frac{\partial}{\partial a_1} \log (1-p) + m \frac{\partial}{\partial a_1} \log p \\ &=& (n-m) \times (-{x_1}p) + m \times {x_1}(1-p) \end{eqnarray}$$

同様に、$\displaystyle \frac{\partial}{\partial a_2} \log L$、$\displaystyle \frac{\partial}{\partial b} \log L$を計算すると、以下のようになる。
$$\begin{eqnarray} \displaystyle \frac{\partial}{\partial a_2} \log L &=& \frac{\partial}{\partial a_2} \left\{ (n-m) \log (1-p) + m \log p \right\} \\ &=& (n-m) \frac{\partial}{\partial a_2} \log (1-p) + m \frac{\partial}{\partial a_2} \log p \\ &=& (n-m) \frac{\partial}{\partial a_2} \left\{ \frac{\partial}{\partial p} \log (1-p) \frac{\partial p}{\partial u} \frac{1}{1 + \exp{(-u)}} \frac{\partial u}{\partial a_2}(b + {a_1}{x_1} + {a_2}{x_2}) \right\} + m \frac{\partial}{\partial a_2} \log p \\ &=& (n-m) \times (-{x_2}p) + m \left\{ \frac{\partial}{\partial p} \log p \frac{\partial p}{\partial u} \frac{1}{1 + \exp{(-u)}} \frac{\partial u}{\partial a_2}(b + {a_1}{x_1} + {a_2}{x_2}) \right\} \\ &=& (n-m) \times (-{x_2}p) + m \times {x_2}(1-p) \\\\ \displaystyle \frac{\partial}{\partial b} \log L &=& \frac{\partial}{\partial b} \left\{ (n-m) \log (1-p) + m \log p \right\} \\ &=& (n-m) \frac{\partial}{\partial b} \log (1-p) + m \frac{\partial}{\partial b} \log p \\ &=& (n-m) \frac{\partial}{\partial b} \left\{ \frac{\partial}{\partial p} \log (1-p) \frac{\partial p}{\partial u} \frac{1}{1 + \exp{(-u)}} \frac{\partial u}{\partial b}(b + {a_1}{x_1} + {a_2}{x_2}) \right\} + m \frac{\partial}{\partial b} \log p \\ &=& (n-m) \times (-p) + m \left\{ \frac{\partial}{\partial p} \log p \frac{\partial p}{\partial u} \frac{1}{1 + \exp{(-u)}} \frac{\partial u}{\partial b}(b + {a_1}{x_1} + {a_2}{x_2}) \right\} \\ &=& (n-m) \times (-p) + m \times (1-p) \end{eqnarray}$$

ここで算出した$\displaystyle \frac{\partial}{\partial a_1} \log L$、$\displaystyle \frac{\partial}{\partial a_2} \log L$、$\displaystyle \frac{\partial}{\partial b} \log L$を利用し、$\displaystyle \frac{\partial}{\partial a_1} \log L = \frac{\partial}{\partial a_2} \log L = \frac{\partial}{\partial b} \log L = 0$となる$a_1$, $a_2$, $b$を算出することになるが、計算で$a_1$, $a_2$, $b$を求めるのは困難なので、最急降下法により算出する。

そのサンプルプログラムについては、以下の記事を参照のこと。

ロジスティクス回帰分析の尤度関数の最適解を算出するクラスを作成してみた 以下の記事で、ロジスティック回帰分析に従う、アヤメがvirginicaである確率$p$の計算式を算出してきた。 https...

要点まとめ

• ロジスティクス回帰分析の対数尤度関数の偏微分では、合成関数の微分・$\log x$の微分・標準シグモイド関数の微分の各公式を利用する。