以下の記事で、ロジスティック回帰分析に従う、アヤメがvirginicaである確率\(p\)の計算式を算出してきた。
(分類を行う)ロジスティック回帰分析の相乗モデルから発生確率を計算してみた 代表的な機械学習フレームワークであるscikit-learnに、アヤメのデータセットが含まれているため、これを利用したアヤメの分類を...
上記記事で算出した確率\(p\)の計算式は、petal length (cm)を\(\mathrm{pl}\)、petal width (cm)を\(\mathrm{pw}\)と記載すると、以下の通り。
\[
\begin{eqnarray}
p &=& \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }} \\\\
p &:& アヤメが\mathrm{virginica}である確率 \\
B &:& 条件0（\mathrm{pl}＜5、かつ、\mathrm{pw}＜1.7）のオッズ \\
A_1 &:& （条件0に対する）条件1（\mathrm{pl}≧5）のオッズ比 \\
x_1 &:& （条件1に対する）0か1の値 \\
A_2 &:& （条件0に対する）条件2（\mathrm{pw}≧1.7）のオッズ比 \\
x_2 &:& （条件2に対する）0か1の値 \\
b &:& \log B \\
a_1 &:& \log A_1 \\
a_2 &:& \log A_2
\end{eqnarray}
\]
また、以下の記事で、ロジスティクス回帰分析の対数尤度関数の偏微分を算出している。
ロジスティクス回帰分析の対数尤度関数を偏微分してみた 以下の記事で、ロジスティック回帰分析に従う、アヤメがvirginicaである確率\(p\)の計算式を算出してきた。 https...
今回は、ロジスティクス回帰分析の対数尤度関数の偏微分の式を利用して、確率\(p\)の最適解\(b\), \(a_1\), \(a_2\)を算出を行い、確率pからアヤメがvirginicaかどうか判定するクラスを作成してみたので、そのサンプルプログラムを共有する。
確率\(p\)の最適解\(b\), \(a_1\), \(a_2\)を算出を行うクラスの内容は、以下の通り。
import numpy as np
import pandas as pd
class OrigLogisticRegressionLine:
# クラス変数
eta = 0.1 # 学習率η
repeat_num = 10000 # 最急降下法の繰り返し回数
# 初期化処理
def __init__(self):
# p=1 / (1 + e^(-(b + a_1*x_1 + a_2*x_2)))のa_1,a_2,bを求めるための初期値を宣言
self.b = 1.0
self.a_1 = 1.0
self.a_2 = 1.0
# 与えられた入力データから、ロジスティクス回帰分析の最適解を算出
def fit(self, data_x, data_y):
# 入力データdata_xから、pl,pwを抽出し変換
data_x_values = self.__input_data_x_trans(data_x)
# 入力データ(y)を、virginica(2)の場合に1、それ以外の場合に0に変換
data_y_values = self.__input_data_y_trans(data_y)
# ロジスティクス回帰分析における、a_1,a_2,bの最適解を算出
self.__logictic_reg(data_x_values, data_y_values)
# 与えられた入力データ(x)から、pl,pwを抽出し変換
def __input_data_x_trans(self, data_x):
# 入力データdata_xから、pl(petal length (cm))、pw(petal width (cm))を取得
data_x_org = data_x[:, -2:]
# 取得したpl(petal length (cm))、pw(petal width (cm))を変換する
# plは、pl≧5の場合1, pl＜5の場合0に、
# pwは、pw≧1.7の場合1, pw＜1.7の場合0に、それぞれ変換する
df_x = pd.DataFrame(data_x_org, columns=['pl', 'pw']).copy()
df_x['pl'].mask(df_x['pl'] < 5, 0, inplace=True)
df_x['pl'].mask(df_x['pl'] >= 5, 1, inplace=True)
df_x['pw'].mask(df_x['pw'] < 1.7, 0, inplace=True)
df_x['pw'].mask(df_x['pw'] >= 1.7, 1, inplace=True)
print("*** 入力データ（pl,pw変換後） ***")
print(df_x.values)
return df_x.values
# 与えられた入力データ(y)を、virginica(2)の場合に1、それ以外の場合に0に変換する
def __input_data_y_trans(self, data_y):
df_y = pd.DataFrame(data_y, columns=['target']).copy()
df_y['target'].mask(df_y['target'] == 1, 0, inplace=True)
df_y['target'].mask(df_y['target'] == 2, 1, inplace=True)
df_y['target'].mask(df_y['target'] != 1, 0, inplace=True)
print("*** 結果データ（target変換後） ***")
print(df_y.values)
print()
return df_y.values
# ロジスティクス回帰分析における、a_1,a_2,bの最適解を算出
def __logictic_reg(self, data_x, data_y):
# 最急降下法をrepeat_num回繰り返す
for num in range(OrigLogisticRegressionLine.repeat_num):
# 各変数の偏微分をそれぞれ算出する
da_1 = 0
da_2 = 0
db = 0
for idx in range(data_x.shape[0]):
u = self.b + self.a_1 * data_x[idx][0] + self.a_2 * data_x[idx][1]
p = 1 / (1 + np.exp(-u))
if data_y[idx] == 1:
da_1 = da_1 + data_x[idx, 0] * (1 - p)
da_2 = da_2 + data_x[idx, 1] * (1 - p)
db = db + (1 - p)
else:
da_1 = da_1 - data_x[idx, 0] * p
da_2 = da_2 - data_x[idx, 1] * p
db = db - p
# 最急降下法により、a_1,a_2,bの値を更新
# 対数尤度関数logLは上に凸のグラフになるため、
# 各変数に、eta*(各変数の偏微分)を加算している
self.a_1 = self.a_1 + OrigLogisticRegressionLine.eta * da_1
self.a_2 = self.a_2 + OrigLogisticRegressionLine.eta * da_2
self.b = self.b + OrigLogisticRegressionLine.eta * db
# 最終結果を出力
print("*** 最終的に算出されたda_1,da_2,db ***")
print("da_1 = " + str(da_1) + ", da_2 = " + str(da_2) + ", db = " + str(db))
print("*** 最終的に算出されたa_1,a_2,b ***")
print("a_1 = " + str(self.a_1) + ", a_2 = " + str(self.a_2)
+ ", b = " + str(self.b))
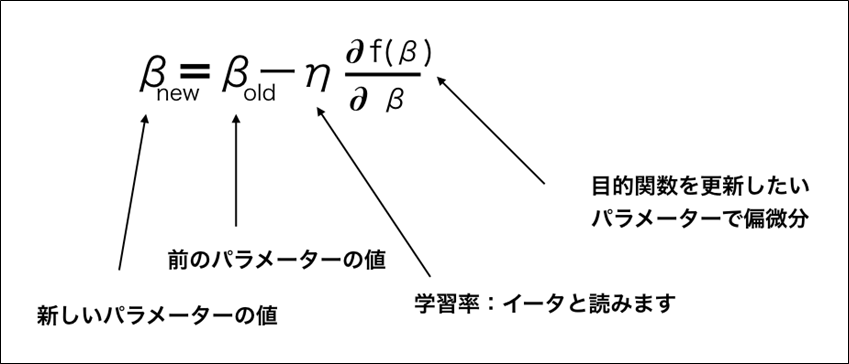
print()上記クラスの「__logictic_reg」メソッドでは、以下の更新式を繰り返しているが、対数尤度関数\(\log L\)は上に凸のグラフになるため、\(η\)の前の符号は＋になっている。
また、上記OrigLogisticRegressionLineクラスのfitメソッドを呼び出して、確率\(p\)の最適解\(b\), \(a_1\), \(a_2\)を算出した結果は、以下の通り。
import numpy as np
from sklearn.datasets import load_iris
# アヤメのデータセットのデータを取得
iris = load_iris()
# 先頭51～55件目のデータ(versicolor)と、先頭101～105件目のデータ(virginica)の
# データを結合し、Xに格納
X = np.append(iris.data[50:55], iris.data[100:105], axis=0)
print("*** 結合した先頭51～55件目と先頭101～105件目のデータ ***")
print(X)
print()
# 先頭51～55件目の結果(versicolor)と、先頭101～105件目の結果(virginica)の
# データを結合し、yに格納
y = np.append(iris.target[50:55], iris.target[100:105], axis=0)
print("*** 結合した先頭51～55件目と先頭101～105件目の結果 ***")
print("*** 判定結果がvirginicaの場合に2、versicolorの場合に1となる ***")
print(y)
print()
# OrigLogisticRegressionLineクラスを使って、ロジスティクス回帰分析の最適解を算出
olr = OrigLogisticRegressionLine()
olr.fit(X, y)
OrigLogisticRegressionLineクラスのfitメソッド呼出時に、入力データの変換を行った結果を出力している。また、「最終的に算出されたda_1,da_2,db」を確認すると、da_1,da_2,dbのいずれも、0に近い値に収束できていることが確認できる。
Code VillageはJavaScriptを中心としたサポート体制が充実したプログラミングスクールだったJavaScriptや、JavaScriptのフレームワーク「React」「Vue」を中心にオンラインで学習できるプログラミングスクール...
さらに、確率\(p\)の最適解\(b\), \(a_1\), \(a_2\)を算出を行うクラスに、確率\(p\)を算出し(\(p\)が\(0.5\)以上かどうかで)判定結果を返却するpredictメソッドを追加した結果は、以下の通り。
import numpy as np
import pandas as pd
class OrigLogisticRegressionLine:
# クラス変数
eta = 0.1 # 学習率η
repeat_num = 10000 # 最急降下法の繰り返し回数
# 初期化処理
def __init__(self):
# p=1 / (1 + e^(-(b + a_1*x_1 + a_2*x_2)))のa_1,a_2,bを求めるための初期値を宣言
self.b = 1.0
self.a_1 = 1.0
self.a_2 = 1.0
# 与えられた入力データから、ロジスティクス回帰分析の最適解を算出
def fit(self, data_x, data_y):
# 入力データdata_xから、pl,pwを抽出し変換
data_x_values = self.__input_data_x_trans(data_x)
# 入力データ(y)を、virginica(2)の場合に1、それ以外の場合に0に変換
data_y_values = self.__input_data_y_trans(data_y)
# ロジスティクス回帰分析における、a_1,a_2,bの最適解を算出
self.__logictic_reg(data_x_values, data_y_values)
# 与えられた入力データ(x)から、判定結果(virginicaかどうか)を返却
def predict(self, data_x):
# 入力データdata_xから、pl,pwを抽出し変換
data_x_values = self.__input_data_x_trans(data_x)
# 入力データをもとに確率pを算出
p_array = np.array([])
for idx in range(data_x_values.shape[0]):
u = self.b + self.a_1 * data_x_values[idx][0] \
+ self.a_2 * data_x_values[idx][1]
p = 1 / (1 + np.exp(-u))
p_array = np.append(p_array, p)
# 小数点以下10桁まで＋指数表記しない形式に設定後、確率を出力
np.set_printoptions(precision=10, suppress=True)
print("*** 判定結果がvirginicaである確率p ***")
print(p_array)
print()
# 算出した確率pから判定結果を返却
# pが0.5以上の場合に1、それ以外の場合に0を返却
return np.where(p_array >= 0.5, 1, 0)
# 与えられた入力データ(x)から、pl,pwを抽出し変換
def __input_data_x_trans(self, data_x):
# 入力データdata_xから、pl(petal length (cm))、pw(petal width (cm))を取得
data_x_org = data_x[:, -2:]
# 取得したpl(petal length (cm))、pw(petal width (cm))を変換する
# plは、pl≧5の場合1, pl＜5の場合0に、
# pwは、pw≧1.7の場合1, pw＜1.7の場合0に、それぞれ変換する
df_x = pd.DataFrame(data_x_org, columns=['pl', 'pw']).copy()
df_x['pl'].mask(df_x['pl'] < 5, 0, inplace=True)
df_x['pl'].mask(df_x['pl'] >= 5, 1, inplace=True)
df_x['pw'].mask(df_x['pw'] < 1.7, 0, inplace=True)
df_x['pw'].mask(df_x['pw'] >= 1.7, 1, inplace=True)
return df_x.values
# 与えられた入力データ(y)を、virginica(2)の場合に1、それ以外の場合に0に変換する
def __input_data_y_trans(self, data_y):
df_y = pd.DataFrame(data_y, columns=['target']).copy()
df_y['target'].mask(df_y['target'] == 1, 0, inplace=True)
df_y['target'].mask(df_y['target'] == 2, 1, inplace=True)
df_y['target'].mask(df_y['target'] != 1, 0, inplace=True)
return df_y.values
# ロジスティクス回帰分析における、a_1,a_2,bの最適解を算出
def __logictic_reg(self, data_x, data_y):
# 最急降下法をrepeat_num回繰り返す
for num in range(OrigLogisticRegressionLine.repeat_num):
# 各変数の偏微分をそれぞれ算出する
da_1 = 0
da_2 = 0
db = 0
for idx in range(data_x.shape[0]):
u = self.b + self.a_1 * data_x[idx][0] + self.a_2 * data_x[idx][1]
p = 1 / (1 + np.exp(-u))
if data_y[idx] == 1:
da_1 = da_1 + data_x[idx, 0] * (1 - p)
da_2 = da_2 + data_x[idx, 1] * (1 - p)
db = db + (1 - p)
else:
da_1 = da_1 - data_x[idx, 0] * p
da_2 = da_2 - data_x[idx, 1] * p
db = db - p
# 最急降下法により、a_1,a_2,bの値を更新
# 対数尤度関数logLは上に凸のグラフになるため、
# 各変数に、eta*(各変数の偏微分)を加算している
self.a_1 = self.a_1 + OrigLogisticRegressionLine.eta * da_1
self.a_2 = self.a_2 + OrigLogisticRegressionLine.eta * da_2
self.b = self.b + OrigLogisticRegressionLine.eta * db
# 最終結果を出力
print("*** 最終的に算出されたda_1,da_2,db ***")
print("da_1 = " + str(da_1) + ", da_2 = " + str(da_2) + ", db = " + str(db))
print("*** 最終的に算出されたa_1,a_2,b ***")
print("a_1 = " + str(self.a_1) + ", a_2 = " + str(self.a_2)
+ ", b = " + str(self.b))
print()また、上記OrigLogisticRegressionLineクラスのfit・predictメソッドを呼び出して、確率pからアヤメがvirginicaかどうか判定した結果は以下の通りで、想定通りの判定結果が返却されていることが確認できる。
import numpy as np
from sklearn.datasets import load_iris
# アヤメのデータセットのデータを取得
iris = load_iris()
# 先頭51～55件目のデータ(versicolor)と、先頭101～105件目のデータ(virginica)の
# データを結合し、Xに格納
X = np.append(iris.data[50:55], iris.data[100:105], axis=0)
print("*** 結合した先頭51～55件目と先頭101～105件目のデータ ***")
print(X)
print()
# 先頭51～55件目の結果(versicolor)と、先頭101～105件目の結果(virginica)の
# データを結合し、yに格納
y = np.append(iris.target[50:55], iris.target[100:105], axis=0)
print("*** 結合した先頭51～55件目と先頭101～105件目の結果 ***")
print("*** 判定結果がvirginicaの場合に2、versicolorの場合に1となる ***")
print(y)
print()
# OrigLogisticRegressionLineクラスを使って、ロジスティクス回帰分析の最適解を算出
olr = OrigLogisticRegressionLine()
olr.fit(X, y)
# 最終的な判定結果を出力
ret = olr.predict(X)
print("*** 結合した先頭51～55件目と先頭101～105件目のデータから判定した結果 ***")
print("*** 判定結果がvirginicaの場合に1、そうでない場合に0となる ***")
print(ret)
要点まとめ
- ロジスティック回帰分析の確率\(p\)の最適解は、対数尤度関数の偏微分を用いて、最急降下法により算出できる。
