代表的な機械学習フレームワークであるscikit-learnに、アヤメのデータセットが含まれているため、これを利用したアヤメの分類を考える。
scikit-learnに含まれるアヤメのデータセットの内容を確認すると、例えば、以下のようになっている。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | from sklearn.datasets import load_iris # アヤメのデータセットのデータを取得 iris = load_iris() print("*** データの構造 ***") print(iris.feature_names) print("*** 結果の構造 ***") print(iris.target_names) print() print("*** データ、結果の要素数 ***") print("データの要素数：" + str(len(iris.data))) print("結果の要素数：" + str(len(iris.target))) print() print("*** 先頭5件のデータ ***") print(iris.data[0:5]) print("*** 先頭5件の結果(setosa) ***") print(iris.target[0:5]) print() print("*** 先頭51～55件目のデータ ***") print(iris.data[50:55]) print("*** 先頭51～55件目の結果(versicolor) ***") print(iris.target[50:55]) print() print("*** 先頭101～105件目のデータ ***") print(iris.data[100:105]) print("*** 先頭101～105件目の結果(virginica) ***") print(iris.target[100:105]) |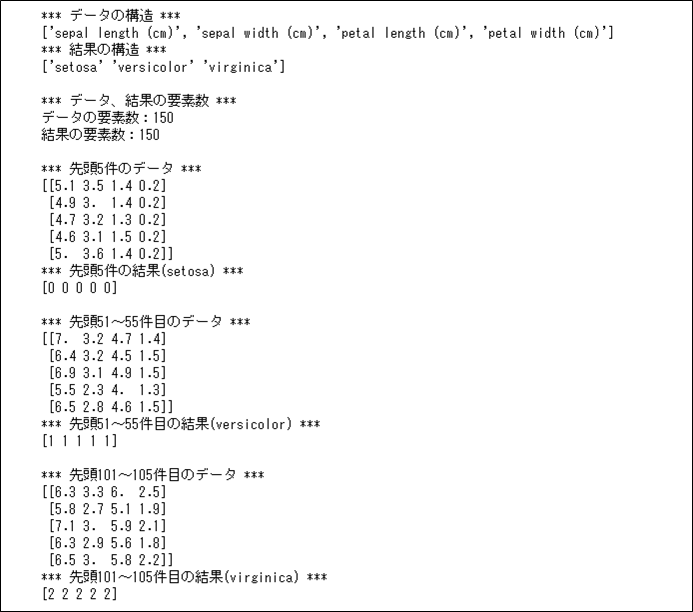
また、このデータから、versicolorとvirginicaの、petal length (cm)とpetal width (cm)の値を一部抜粋してグラフ化した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | %matplotlib inline import matplotlib.pyplot as plt from sklearn.datasets import load_iris # アヤメのデータセットのデータを取得 iris = load_iris() # 先頭51～55件目のデータ(versicolor)の # petal length (cm)、petal width (cm)を取得 ver_petal_length = iris.data[50:55, 2] ver_petal_width = iris.data[50:55, 3] print("*** 先頭51～55件目のpetal length (cm) ***") print(ver_petal_length) print("*** 先頭51～55件目のpetal width (cm) ***") print(ver_petal_width) # 先頭101～105件目のデータ(virginica)の # petal length (cm)、petal width (cm)を取得 vir_petal_length = iris.data[100:105, 2] vir_petal_width = iris.data[100:105, 3] print("*** 先頭101～105件目のpetal length (cm) ***") print(vir_petal_length) print("*** 先頭101～105件目のpetal width (cm) ***") print(vir_petal_width) # 抽出した結果を散布図で表示 plt.scatter(ver_petal_length, ver_petal_width, label="versicolor") plt.scatter(vir_petal_length, vir_petal_width, label="virginica") plt.title("iris data") plt.xlabel("petal length (cm)", size=14) plt.ylabel("petal width (cm)", size=14) plt.xlim(3, 7) plt.ylim(1, 3) plt.legend() plt.grid() plt.show() |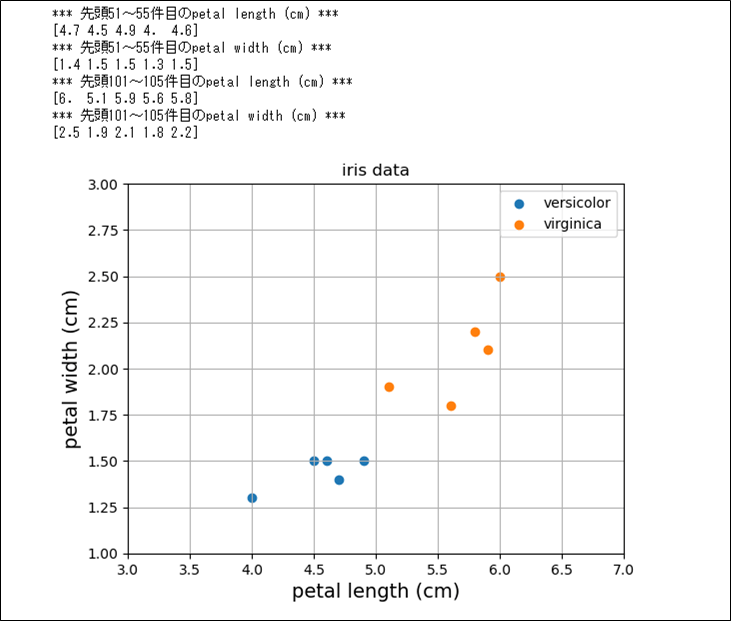
この図を見ると、petal length (cm)が5以上でpetal width (cm)が1.7以上だとvirginicaで、そうでないとversicolorと分類できそうである。
このような分類を行う手法の1つに、ロジスティック回帰分析がある。
ロジスティック回帰分析とは、いくつかの要因（説明変数）から「2値の結果（目的変数）」が起こる確率を説明・予測することができる統計手法のことをいい、いくつかの要因（説明変数）をオッズで表現することで、その確率を計算することができる。
例えば、petal length (cm)【下表ではpl】が5以上か、petal width (cm)【下表ではpw】が1.7以上かどうかの2つの条件下で、アヤメがvirginicaである株数を仮設定して、アヤメがvirginicaである確率やオッズ・オッズ比を計算すると、以下のようになる。
| 説明変数 | virginica？ | アヤメが virginicaで ある確率 | アヤメが virginicaである 場合のオッズ | （条件0に 対する） オッズ比 | |||
|---|---|---|---|---|---|---|---|
| pl ≧5？ | pw ≧1.7？ | Yes (株) | No (株) | ||||
| 条件0 | No | No | \(1\) | \(10\) | \(\displaystyle \frac{1}{1+10} = \frac{1}{11}\) | \(\frac{\displaystyle \frac{1}{11}}{\displaystyle \frac{10}{11}}=\displaystyle \frac{1}{10}(=B)\) | – |
| 条件1 | Yes | No | \(16\) | \(10\) | \(\displaystyle \frac{16}{16+10} = \frac{16}{26}\) | \(\displaystyle \frac{16}{10} = B \times 16\) | \(16\) |
| 条件2 | No | Yes | \(15\) | \(10\) | \(\displaystyle \frac{15}{15+10} = \frac{15}{25}\) | \(\displaystyle \frac{15}{10} = B \times 15\) | \(15\) |
なお、virginicaの確率やオッズは、以下の式で計算できる。
（アヤメがvirginicaである確率）＝ （virginicaの株数）／（全体の株数）
（アヤメがvirginicaである場合のオッズ）
＝（アヤメがvirginicaである確率）／（1 -（アヤメがvirginicaである確率））
＝（アヤメがvirginicaである株数）／（アヤメがvirginicaでない株数）
これを一般化すると、以下のように表現できる。
| 説明変数 | virginica？ | アヤメが virginicaで ある確率 | アヤメが virginicaである 場合のオッズ | （条件0に 対する） オッズ比 | |||
|---|---|---|---|---|---|---|---|
| pl ≧5？ | pw ≧1.7？ | Yes (株) | No (株) | ||||
| 条件0 | No | No | \(c_0\) | \(d_0\) | \(\displaystyle \frac{c_0}{c_0+d_0}\) | \(\frac{\displaystyle \frac{c_0}{c_0+d_0}}{\displaystyle \frac{d_0}{c_0+d_0}} = \displaystyle \frac{c_0}{d_0}(=B)\) | – |
| 条件1 | Yes | No | \(c_1\) | \(d_1\) | \(\displaystyle \frac{c_1}{c_1+d_1}\) | \(\displaystyle \frac{c_1}{d_1} = B \times A_1\) | \(A_1\) |
| 条件2 | No | Yes | \(c_2\) | \(d_2\) | \(\displaystyle \frac{c_2}{c_2+d_2}\) | \(\displaystyle \frac{c_2}{d_2} = B \times A_2\) | \(A_2\) |
さらに、リスク要因が複数あるとき、ある事象の発生確率を個々のリスクのオッズ比の積で表せると仮定すると、条件3の各値は、以下のように表現できる。
| 説明変数 | virginica？ | アヤメが virginicaで ある確率 | アヤメが virginicaである 場合のオッズ | （条件0に 対する） オッズ比 | |||
|---|---|---|---|---|---|---|---|
| pl ≧5？ | pw ≧1.7？ | Yes (株) | No (株) | ||||
| 条件3 | Yes | Yes | \(c_3\) | \(d_3\) | \(\displaystyle \frac{c_3}{c_3+d_3}\) | \(\displaystyle \frac{c_3}{d_3} = B \times A_1 \times A_2\) | \(A_1 \times A_2\) |
以上より、条件0～条件3のオッズをまとめると、以下の式で表される。
\[
\begin{eqnarray}
\displaystyle \frac{p}{1-p} &=& B \times {A_1}^{x_1} \times {A_2}^{x_2} \\\\
p &:& アヤメが\mathrm{virginica}である確率 \\
B &:& 条件0（\mathrm{pl}＜5、かつ、\mathrm{pw}＜1.7）のオッズ \\
A_1 &:& （条件0に対する）条件1（\mathrm{pl}≧5）のオッズ比 \\
x_1 &:& （条件1に対する）0か1の値 \\
A_2 &:& （条件0に対する）条件2（\mathrm{pw}≧1.7）のオッズ比 \\
x_2 &:& （条件2に対する）0か1の値
\end{eqnarray}
\]
前述の\(\displaystyle \frac{p}{1-p} = B \times {A_1}^{x_1} \times {A_2}^{x_2}\)の両辺に自然対数をとり、式変形していく。
\[
\begin{eqnarray}
\log \displaystyle \frac{p}{1-p} &=& \log \left( B \times {A_1}^{x_1} \times {A_2}^{x_2} \right) \\
&=& \log B + \log {A_1}^{x_1} + \log {A_2}^{x_2} \\
&=& \log B + {x_1}\log {A_1} + {x_2}\log {A_2} \\
&=& \log B + \log {A_1} \times {x_1} + \log {A_2} \times {x_2}
\end{eqnarray}
\]
\(Y = \log B + \log {A_1} \times {x_1} + \log {A_2} \times {x_2}\)と置き換え、式変形していく。
\[
\begin{eqnarray}
\log \displaystyle \frac{p}{1-p} &=& Y \\
\displaystyle \frac{p}{1-p} &=& e^Y \\
p &=& (1-p)e^Y \\
p &=& e^Y – pe^Y \\
p + pe^Y &=& e^Y \\
p(1 + e^Y) &=& e^Y \\
p &=& \displaystyle \frac{e^Y}{1 + e^Y} \\
&=& \displaystyle \frac{1}{e^{-Y} + 1} \\
&=& \displaystyle \frac{1}{1 + e^{-Y}} \\
&=& \displaystyle \frac{1}{1 + \exp(-Y)} \\
&=& \displaystyle \frac{1}{1 + \exp{ \{ -(\log B + \log {A_1} \times {x_1} + \log {A_2} \times {x_2}) \} }}
\end{eqnarray}
\]
ここで、\(b = \log B\)、\(a_1 = \log {A_1}\)、\(a_2 = \log {A_2}\)と置き換えると、
\[
\begin{eqnarray}
p = \displaystyle \frac{1}{1 + \exp{ \{ -(b + {a_1}{x_1} + {a_2}{x_2}) \} }}
\end{eqnarray}
\]
となり、シグモイド関数の数式となる。
例えば、\(B=0.1\)、\(A_1=16\)、\(A_2=15\)とした場合の確率pの値を計算した結果は、以下のようになる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | import numpy as np # シグモイド関数の値を計算 def sigmoid(a): s = 1 / (1 + np.e**(-a)) return s # 確率を計算 def prob(x_1, x_2, A_1, A_2): Y = np.log(0.1) + np.log(A_1) * x_1 + np.log(A_2) * x_2 return sigmoid(Y) B = 0.1 # 条件0(pl＜5、かつ、pw＜1.7)のオッズ A_1 = 16 # (条件0に対する)条件1(pl≧5)のオッズ比 A_2 = 15 # (条件0に対する)条件2(pw≧1.7)のオッズ比 print("B = " + str(B) + ", A_1 = " + str(A_1) + ", A_2 = " + str(A_2)) # B, A_1, A_2の、e(≒2.7)を底とする対数 b = np.log(B) a_1 = np.log(A_1) a_2 = np.log(A_2) print("b = " + str(b) + ", a_1 = " + str(a_1) + ", a_2 = " + str(a_2)) print() print("*** x_1, x_2の値に応じた確率を計算した結果 ***") # x_1=0, x_2=0の場合の確率 x_1 = 0 x_2 = 0 p = prob(x_1, x_2, A_1, A_2) print("x_1 = " + str(x_1) + ", x_2 = " + str(x_2) + ", p = " + str(p)) # x_1=1, x_2=0の場合の確率 x_1 = 1 x_2 = 0 p = prob(x_1, x_2, A_1, A_2) print("x_1 = " + str(x_1) + ", x_2 = " + str(x_2) + ", p = " + str(p)) # x_1=0, x_2=1の場合の確率 x_1 = 0 x_2 = 1 p = prob(x_1, x_2, A_1, A_2) print("x_1 = " + str(x_1) + ", x_2 = " + str(x_2) + ", p = " + str(p)) # x_1=1, x_2=1の場合の確率 x_1 = 1 x_2 = 1 p = prob(x_1, x_2, A_1, A_2) print("x_1 = " + str(x_1) + ", x_2 = " + str(x_2) + ", p = " + str(p)) |
要点まとめ
- ロジスティック回帰分析とは、いくつかの要因（説明変数）から「2値の結果（目的変数）」が起こる確率を説明・予測することができる統計手法のことをいう。
- （オッズ）＝（発生確率）／（1 -（発生確率））で表現できる。
- オッズから発生確率を計算すると、シグモイド関数の数式となる。
