格差を数値で表現したものがジニ係数で、ジニ係数を計算前の関係性をグラフ化したものがローレンツ曲線である。
今回は、「令和3年所得再分配調査報告書」のデータを用いて、ローレンツ曲線の描画とジニ係数の計算をしてみたので、そのサンプルプログラムを共有する。
なお、ジニ係数とローレンツ曲線については、以下のサイトを参照のこと。
https://sdgs-compass.jp/column/4409
前提条件
下記記事のAnacondaをインストールしJupyter Notebookを利用できること
Python開発用のAnacondaをインストールしJupyter Notebookを利用してみた今回は、Pythonを勉強してみたいと思い、Python開発環境を構築してみたので、その手順を共有する。 Python開発用として...
また、以下の「令和3年所得再分配調査報告書」の表1「所得再分配による十分位階級別所得構成比の変化」に記載の、令和3年のデータを用いるものとする。
ローレンツ曲線の描画
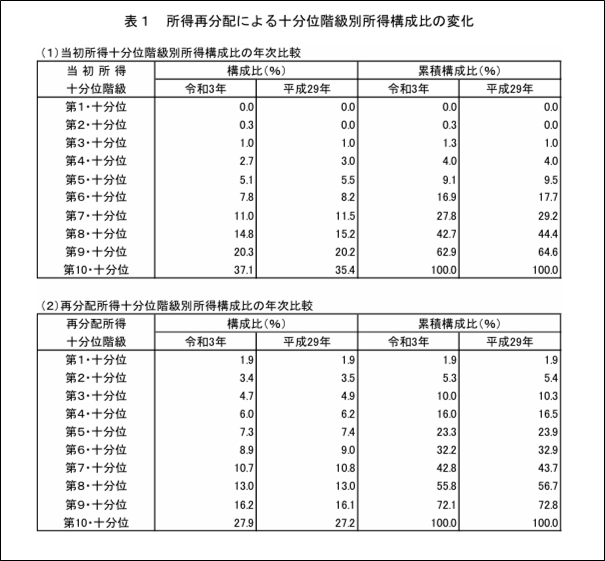
表1「所得再分配による十分位階級別所得構成比の変化」の令和3年のデータを、ローレンツ曲線に描画した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 所得_十分位階級 x = np.linspace(0, 1, 11) # 令和3年_当初_累積構成比 y_1 = np.array([0, 0, 0.3, 1.3, 4, 9.1, 16.9, 27.8, 42.7, 62.9, 100])*0.01 # 令和3年_再配分_累積構成比 y_2 = np.array([0, 1.9, 5.3, 10.0, 16.0, 23.3, 32.2, 42.8, 55.8, 72.1, 100])*0.01 # 完全平等線 y_3 = np.linspace(0, 1, 11) # x,y_1,y_2,y_3の各値を出力 print("*** 所得_十分位階級(x) ***") print(x) print("*** 令和3年_当初_累積構成比(y_1) ***") print(y_1) print("*** 令和3年_再配分_累積構成比(y_2) ***") print(y_2) print("*** 完全平等線(y_3) ***") print(y_3) print() # (x,y_1),(x,y_2),(x,y_3)それぞれをグラフに描画 plt.plot(x, y_1, label="reiwa 3 origin", color="green") plt.plot(x, y_2, label="reiwa 3 reallocate", color="blue") plt.plot(x, y_3, linestyle = "dashed", label="perfect equality line", color="orange") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.grid() plt.legend() plt.show() |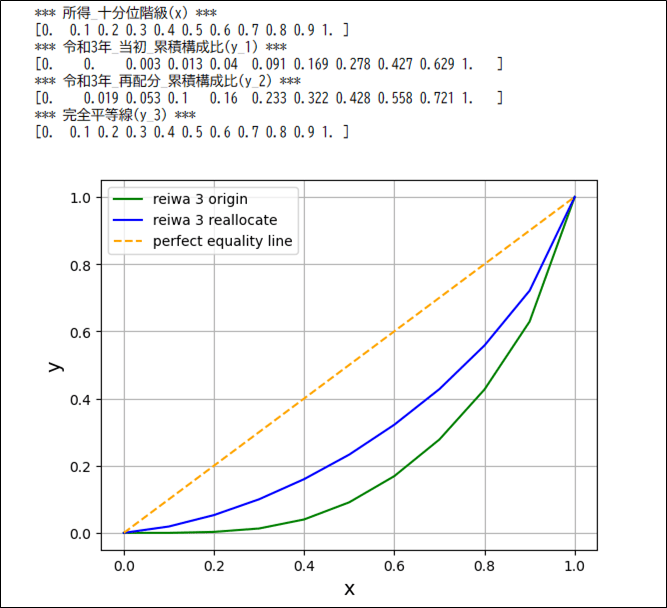
Androidロックを解除する裏ワザ「4uKey for Android」をご紹介Android端末では、以下の画像のような画面ロックパスワードを設定することができますが、このパスワードを忘れてしまうと、Android...
integrate.trapzを利用した面積の計算
Scipyのintegrate.trapz関数を利用すると、折れ線グラフとx軸で挟まれた部分の面積を求めることができる。その算出例は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | %matplotlib inline from scipy import integrate import numpy as np import matplotlib.pyplot as plt # 所得_十分位階級 x = np.linspace(0, 1, 11) # 完全平等線 y_3 = np.linspace(0, 1, 11) # 完全平等線をグラフに描画し、完全平等線とx軸で挟まれた部分を塗りつぶして表示 plt.plot(x, y_3, linestyle = "dashed", label="perfect equality line", color="orange") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.grid() plt.legend() plt.fill_between(x, y_3, fc="lightblue") plt.show() # integrate.trapzを利用し、完全平等線とx軸で挟まれた部分の面積を算出 print("*** 完全平等線とx軸で挟まれた部分の面積 ***") print("*** 手動計算(1.0×1.0÷2)の場合 ***") print(1.0*1.0/2) print("*** integrate.trapzを利用した場合 ***") print(integrate.trapz(y_3, x)) |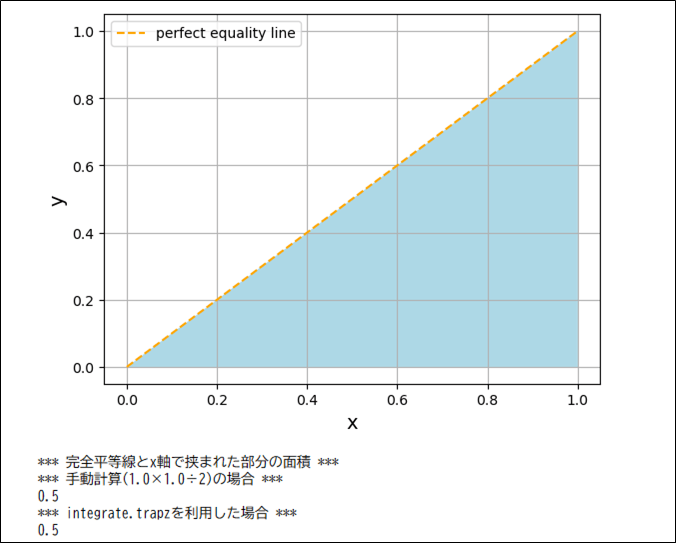
ジニ係数の計算
表1「所得再分配による十分位階級別所得構成比の変化」の令和3年のデータから、ジニ係数を計算した結果は以下の通りで、（社会保障制度及び租税制度による）所得再分配により、ジニ係数が小さくなっていることが確認できる。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | %matplotlib inline from scipy import integrate import numpy as np import matplotlib.pyplot as plt # 所得_十分位階級 x = np.linspace(0, 1, 11) # 令和3年_当初_累積構成比 y_1 = np.array([0, 0, 0.3, 1.3, 4, 9.1, 16.9, 27.8, 42.7, 62.9, 100])*0.01 # 完全平等線 y_3 = np.linspace(0, 1, 11) # 令和3年_当初_累積構成比, 完全平等線をグラフに描画し、 # 完全平等線と令和3年_当初_累積構成比で挟まれた部分を塗りつぶして表示 plt.plot(x, y_1, label="reiwa 3 origin", color="green") plt.plot(x, y_3, linestyle = "dashed", label="perfect equality line", color="orange") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.grid() plt.legend() plt.fill_between(x, y_1, y_3, fc="lightblue") plt.show() # integrate.trapzを利用し、ジニ係数(完全平等線と令和3年_当初_累積構成比で挟まれた部分の面積×2)を算出 print("*** ジニ係数(完全平等線と令和3年_当初_累積構成比で挟まれた部分の面積×2) ***") print((0.5 - integrate.trapz(y_1, x))*2) |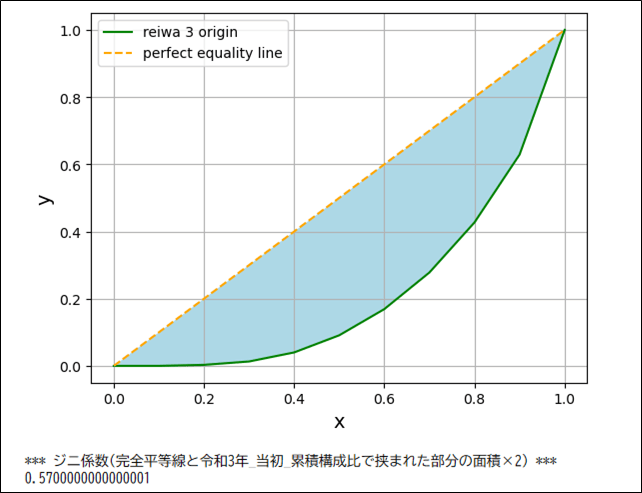
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | %matplotlib inline from scipy import integrate import numpy as np import matplotlib.pyplot as plt # 所得_十分位階級 x = np.linspace(0, 1, 11) # 令和3年_再配分_累積構成比 y_2 = np.array([0, 1.9, 5.3, 10.0, 16.0, 23.3, 32.2, 42.8, 55.8, 72.1, 100])*0.01 # 完全平等線 y_3 = np.linspace(0, 1, 11) # 令和3年_再配分_累積構成比, 完全平等線をグラフに描画し、 # 完全平等線と令和3年_再配分_累積構成比で挟まれた部分を塗りつぶして表示 plt.plot(x, y_2, label="reiwa 3 reallocate", color="blue") plt.plot(x, y_3, linestyle = "dashed", label="perfect equality line", color="orange") plt.xlabel("x", size=14) plt.ylabel("y", size=14) plt.grid() plt.legend() plt.fill_between(x, y_2, y_3, fc="lightblue") plt.show() # integrate.trapzを利用し、ジニ係数(完全平等線と令和3年_再配分_累積構成比で挟まれた部分の面積×2)を算出 print("*** ジニ係数(完全平等線と令和3年_再配分_累積構成比で挟まれた部分の面積×2) ***") print((0.5 - integrate.trapz(y_2, x))*2) |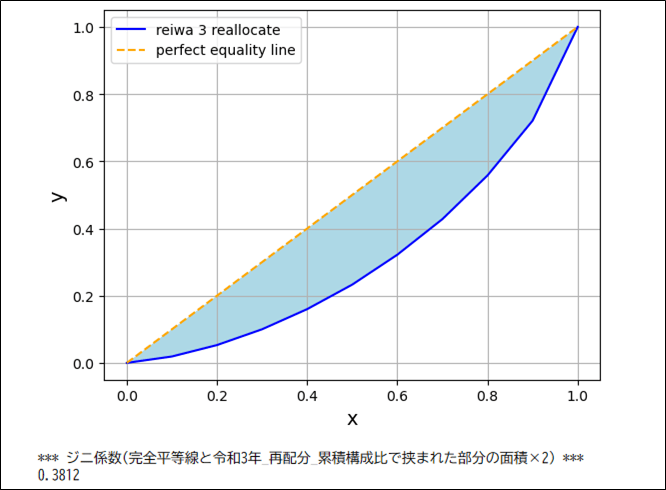
要点まとめ
- 格差を数値で表現したものがジニ係数で、ジニ係数を計算前の関係性をグラフ化したものがローレンツ曲線である。
- ジニ係数を計算する際の面積は、Scipyのintegrate.trapz関数を利用して計算できる。
