PythonのMatplotlibライブラリを利用すると、様々な関数のグラフを描くことができる。今回は、1次関数や2次関数のグラフを描いてみたので、そのサンプルプログラムを共有する。
前提条件
下記記事のAnacondaをインストールしJupyter Notebookを利用できること
Python開発用のAnacondaをインストールしJupyter Notebookを利用してみた今回は、Pythonを勉強してみたいと思い、Python開発環境を構築してみたので、その手順を共有する。 Python開発用として...
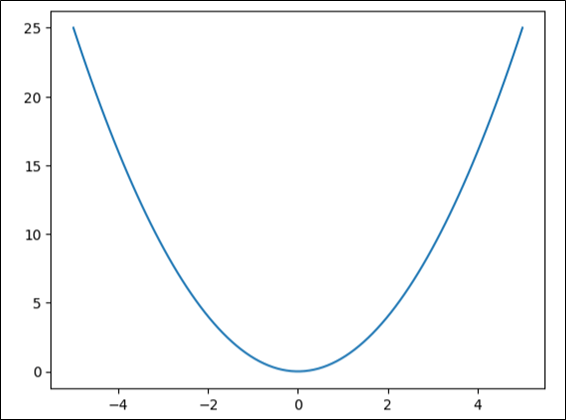
\(y=x^2\)のグラフ
\(y=x^2\)のグラフを描くソースコードの内容は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt def f(x): return x**2 # -5～5までを100等分した値をxとする x = np.linspace(-5, 5, 100) # 上記xに対応するyの値(=xの2乗)を算出 y = f(x) # x,yに対応する値のグラフを表示 plt.plot(x, y) plt.show() |
上記ソースコードを実行した結果は、以下の通り。
NumPyライブラリのlinspace関数を利用すると、(第一引数)～(第二引数)までを(第三引数)等分した値を生成できる。例えば、以下の例では、0～1までを10等分した値を表示している。
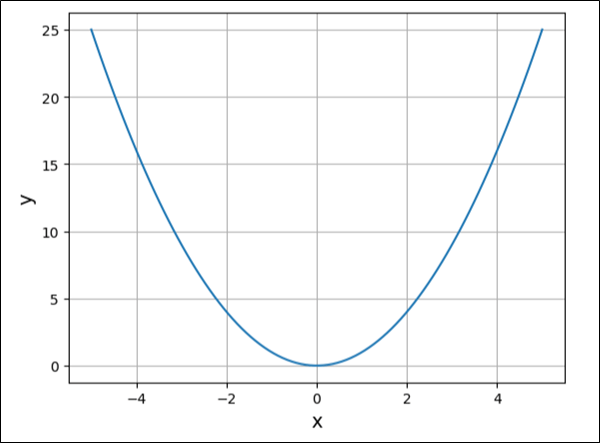
1 2 3 4 5 6 7 8 9 10 11 | import numpy as np # np.linspace関数の利用 # 下記例では、0～1までを10等分した値を生成している x = np.linspace(0, 1, 10) print("*** np.linspace関数で分割後のxの値 ***") print(x) print() print("*** np.linspace関数で分割後のxの要素数 ***") print(x.shape) |
＜実行結果＞
その他、\(y=x^2\)のグラフに、x軸・y軸のラベルやグリッド線を追加した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt def f(x): return x**2 # -5～5までを100等分した値をxとする x = np.linspace(-5, 5, 100) # 上記xに対応するyの値(=xの2乗)を算出 y = f(x) # x,yに対応する値を設定 plt.plot(x, y) # x軸・y軸のラベルを表示 plt.xlabel("x", size=14) plt.ylabel("y", size=14) # グリッド線を表示 plt.grid() # x,yに対応する値のグラフを表示 plt.show() |
＜実行結果＞
「EaseUS Todo Backup」は様々な形でバックアップ取得が行える便利ツールだったパソコン内のデータを、ファイル/パーティション/ディスク等の様々な単位でバックアップしたり、バックアップのスケジュール設定や暗号化設定も...
1次関数のグラフの追加
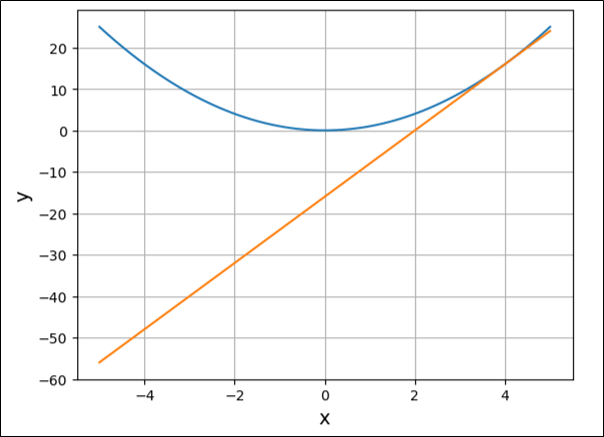
\(y=x^2\)のグラフに、このグラフのx=4における接線(\(y=8x-6\))をそのまま追加したソースコードは、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt def f(x): return x**2 def d_f4(x): return 8 * x - 16 # -5～5までを100等分した値をxとする x = np.linspace(-5, 5, 100) # 上記xに対応するyの値(=xの2乗)を算出 y = f(x) # 上記関数の、x=4における接線 y_df4 = d_f4(x) # x,y,y_df4に対応する値を設定 plt.plot(x, y) plt.plot(x, y_df4) # x軸・y軸のラベルを表示 plt.xlabel("x", size=14) plt.ylabel("y", size=14) # グリッド線を表示 plt.grid() # x,yに対応する値のグラフを表示 plt.s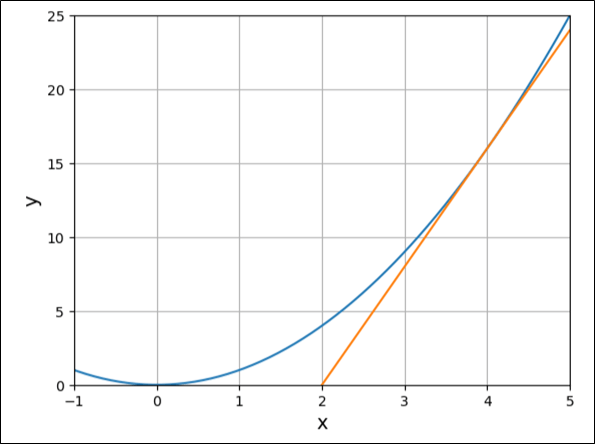how() |
＜実行結果＞
このグラフの表示範囲を、x軸を-1～5、y軸を0～25に変更したソースコードと実行結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt def f(x): return x**2 def d_f4(x): return 8 * x - 16 # -5～5までを100等分した値をxとする x = np.linspace(-5, 5, 100) # 上記xに対応するyの値(=xの2乗)を算出 y = f(x) # 上記関数の、x=4における接線 y_df4 = d_f4(x) # x,y,y_df4に対応する値を設定 plt.plot(x, y) plt.plot(x, y_df4) # x軸・y軸のラベルを表示 plt.xlabel("x", size=14) plt.ylabel("y", size=14) # x軸・y軸の表示範囲を指定 plt.xlim(-1, 5) plt.ylim(0, 25) # グリッド線を表示 plt.grid() # x,yに対応する値のグラフを表示 plt.show() |
＜実行結果＞
要点まとめ
- PythonのMatplotlibライブラリを利用すると、様々な関数のグラフを描くことができる。
- PythonのNumPyライブラリのlinspace関数を利用すると、(第一引数)～(第二引数)までを(第三引数)等分した値を生成できる。
- 関数の引数に、NumPyライブラリで生成した1次元配列を渡すと、その引数の各値に対応する値を返却できる。
