これまでは、ニューラルネットワークの活性化関数にシグモイド関数を利用してきたが、偏微分の計算ができれば、活性化関数にシグモイド関数以外も利用することができる。
今回は、ニューラルネットワークの活性化関数にtanh関数を利用してみたので、そのサンプルプログラムを共有する。
前提条件
以下の記事の実装が完了していること。

今回実装するニューラルネットワークの全体構成は、以下のようになる。
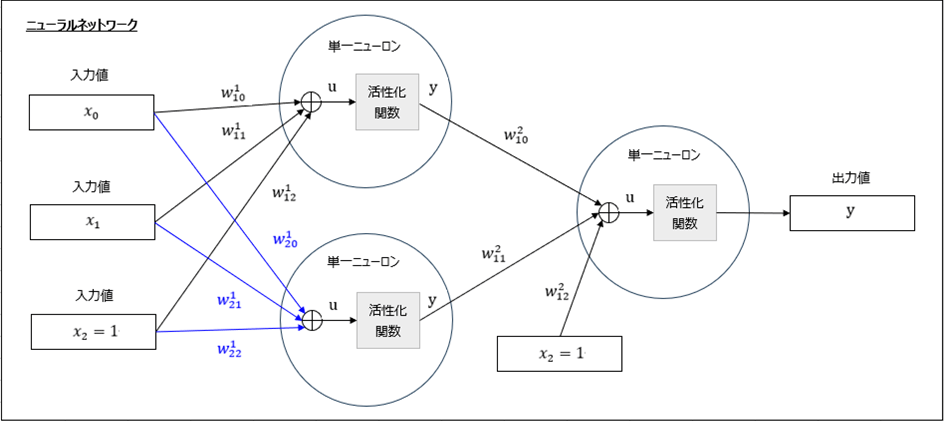
また、重み\(\boldsymbol w\)の最適解は、下図における誤差関数\(E=(x_3 – y)^2\)が最小となる箇所で、これは誤差関数を(桃枠の)各変数について偏微分した結果が\(0\)になる値となる。
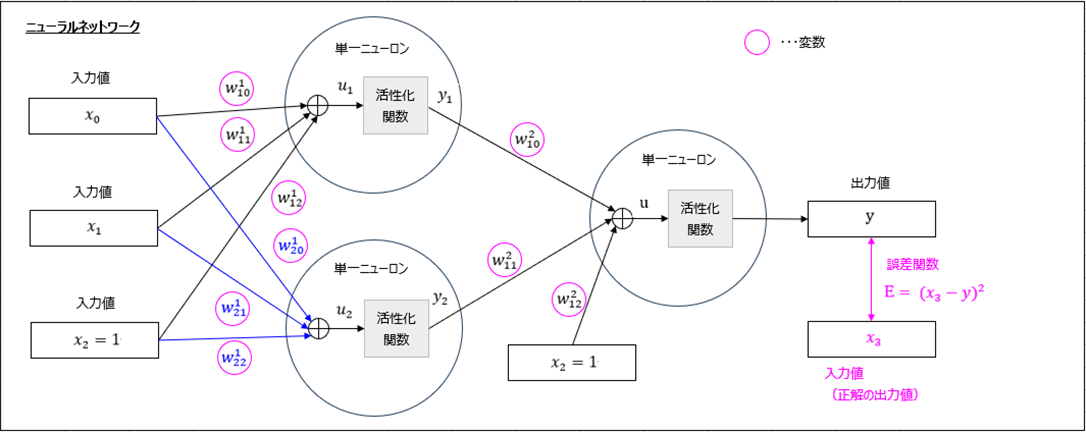
このうち、単一ニューロンを実装した内容は以下の通りで、前提条件の記事の、フォワードプロパゲーションを行うメソッド(forward)で、tanh関数を利用している。
import numpy as np
# 単一ニューロン
class OrigNeuron:
# クラス変数
eta = 0.1 # 学習率η
# 変数の初期化
def __init__(self):
# 入力データ(変数x)
self.x = np.array([])
# 入力データ(重みw)
self.w = np.array([])
# 出力データ(シグモイド関数の変換前)
self.u = 0
# 出力データ
self.y = 0
# 入力データ(変数x、重みw:いずれもNumpy配列)の設定
def set_input_data(self, x, w):
if self.__input_check(x, 2) and self.__input_check(w, 3):
self.x = x
self.w = w
else:
print("OrigNeuron set_input_data : 引数の指定方法が誤っています")
# フォワードプロパゲーションで出力変数を設定
def forward(self):
if self.__input_check(self.x, 2) and self.__input_check(self.w, 3):
self.u = self.x[0] * self.w[0] + self.x[1] * self.w[1] + self.w[2]
self.y = self.__tanh(self.u)
# バックプロパゲーションで入力データ(重みw)を変更
def back(self, dw):
if self.__input_check(dw, 3):
# 引数の偏微分を利用して、最急降下法により、重みwの値を更新する
self.w = self.w - OrigNeuron.eta * dw
# 出力データyを返却
def get_y(self):
return self.y
# 出力データ(シグモイド関数の変換前)uを返却
def get_u(self):
return self.u
# 重みwを返却
def get_w(self):
return self.w
# 入力データの型・長さをチェック
def __input_check(self, data, size):
if isinstance(data, np.ndarray) and len(data) == size:
if np.issubdtype(data.dtype, float) or np.issubdtype(data.dtype, int):
return True
return False
return False
# tanh関数による変換
def __tanh(self, data):
return (np.e**(data) - np.e**(-data)) / (np.e**(data) + np.e**(-data))
また、ニューラルネットワークを実装した内容は以下の通りで、前提条件の記事の、バックプロパゲーションを行うメソッド(back)で設定する偏微分を、tanh関数に対応したものにしている。
import numpy as np
# ニューラルネットワーク
class OrigNeuralNetwork:
# クラス変数
repeat_num = 10000 # 最急降下法の繰り返し回数
# 変数の初期化
# 変数x、重みw、重みの微分dw:いずれもNumpy配列 の設定
# ニューロンの生成と初期値の代入
def __init__(self, x):
if self.__input_check(x, 3):
self.x = x[:-1] # 入力値x_0,x_1
self.x_3 = x[-1:] # 入力値x_3(正解値)
self.w = np.array([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0], [1.0, 1.0, 1.0]])
self.dw = np.array([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0], [1.0, 1.0, 1.0]])
# ニューロンの生成と初期値の代入
self.on11 = OrigNeuron()
self.on11.set_input_data(self.x, self.w[0])
self.on12 = OrigNeuron()
self.on12.set_input_data(self.x, self.w[1])
self.on21 = OrigNeuron()
self.on21.set_input_data(np.array([self.on11.get_y(), self.on12.get_y()])
, self.w[2])
else:
self.x = np.array([])
print("OrigNeuralNetwork set_input_data : 引数の指定方法が誤っています")
# フォワードプロパゲーションとバックプロパゲーションを繰り返す
def repeat_forward_back(self):
for num in range(OrigNeuralNetwork.repeat_num):
self.forward()
self.back()
# フォワードプロパゲーションで出力変数を設定
def forward(self):
if self.__input_check(self.x, 2):
self.on11.forward()
self.on12.forward()
self.on21.forward()
# バックプロパゲーションで重み、出力変数を変更
def back(self):
if self.__input_check(self.x, 2):
# 後続の偏微分を計算する際に必要なtanh関数の微分を定義
self.on21_d_tanh = self.__diff_tanh(self.on21.get_u())
self.on11_d_tanh = self.__diff_tanh(self.on11.get_u())
self.on12_d_tanh = self.__diff_tanh(self.on12.get_u())
# 後続の偏微分を計算する際の共通部分を定義
self.d_com = 2 * (self.on21.get_y() - self.x_3[0]) * self.on21_d_tanh
# w^1_10, w^1_11, w^1_12についての偏微分を計算し、重みw[0]を更新
self.dw[0][0] = self.d_com * self.w[2][0] * self.on11_d_tanh * self.x[0]
self.dw[0][1] = self.d_com * self.w[2][0] * self.on11_d_tanh * self.x[1]
self.dw[0][2] = self.d_com * self.w[2][0] * self.on11_d_tanh
self.on11.back(self.dw[0])
self.w[0] = self.on11.get_w()
# w^1_20, w^1_21, w^1_22についての偏微分を計算し、重みw[1]を更新
self.dw[1][0] = self.d_com * self.w[2][1] * self.on12_d_tanh * self.x[0]
self.dw[1][1] = self.d_com * self.w[2][1] * self.on12_d_tanh * self.x[1]
self.dw[1][2] = self.d_com * self.w[2][1] * self.on12_d_tanh
self.on12.back(self.dw[1])
self.w[1] = self.on12.get_w()
# w^2_10, w^2_11, w^2_12についての偏微分を計算し、重みw[2]を更新
self.dw[2][0] = self.d_com * self.on11.get_y()
self.dw[2][1] = self.d_com * self.on12.get_y()
self.dw[2][2] = self.d_com
self.on21.back(self.dw[2])
self.w[2] = self.on21.get_w()
# 出力データを返却
def get_y(self):
if self.__input_check(self.x, 2):
return self.on21.get_y()
else:
return None
# 入力データの型・長さをチェック
def __input_check(self, data, size):
if isinstance(data, np.ndarray) and len(data) == size:
if np.issubdtype(data.dtype, float) or np.issubdtype(data.dtype, int):
return True
return False
return False
# tanh関数の微分の定義
def __diff_tanh(self, data):
return 4.0 / (np.e**(data) + np.e**(-data))**2なお、backメソッドで利用している重み\(\boldsymbol w\)の各変数の偏微分を計算する際、以下の計算結果も利用するものとする。
\[
\begin{eqnarray}
\mathrm{tanh}(x) &=& \displaystyle \frac{e^x – e^{-x}}{e^x + e^{-x}} \\
\mathrm{dtanh}(x) &=& \displaystyle \frac{d}{dx} \mathrm{tanh}(x) = \frac{4}{({e^x + e^{-x}})^2} \\
u_1 &=& x_0 \times w^1_{10} + x_1 \times w^1_{11} + 1 \times w^1_{12} \\
y_1 &=& \mathrm{tanh}(u_1) \\
u_2 &=& x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22} \\
y_2 &=& \mathrm{tanh}(u_2) \\
u &=& y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12} \\
y &=& \mathrm{tanh}(u)
\end{eqnarray}
\]
実際に、誤差関数を、重みの各変数についての偏微分を計算した結果は、以下の通り。
\[
\begin{multline}
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{10}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_1}
\frac{\partial y_1}{\partial u_1} \frac{\partial u_1}{\partial w^1_{10}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial y_1}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ \times \frac{\partial}{\partial u_1}\mathrm{tanh}(u_1) \times
\frac{\partial}{\partial w^1_{10}}(x_0 \times w^1_{10} + x_1 \times w^1_{11} + 1 \times w^1_{12}) } \\
\shoveleft{ = 2(x_3 – y) \times (-1) \times \mathrm{dtanh}(u) \times w^2_{10} \times \mathrm{dtanh}(u_1) \times x_0 } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{10} \times \mathrm{dtanh}(u_1) \times x_0 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{11}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_1}
\frac{\partial y_1}{\partial u_1} \frac{\partial u_1}{\partial w^1_{11}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial y_1}(y_1 \times w^2_{11} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ \times \frac{\partial}{\partial u_1}\mathrm{tanh}(u_1) \times
\frac{\partial}{\partial w^1_{11}}(x_0 \times w^1_{11} + x_1 \times w^1_{11} + 1 \times w^1_{12}) } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{10} \times \mathrm{dtanh}(u_1) \times x_1 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{12}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_1}
\frac{\partial y_1}{\partial u_1} \frac{\partial u_1}{\partial w^1_{12}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial y_1}(y_1 \times w^2_{11} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ \times \frac{\partial}{\partial u_1}\mathrm{tanh}(u_1) \times
\frac{\partial}{\partial w^1_{12}}(x_0 \times w^1_{11} + x_1 \times w^1_{11} + 1 \times w^1_{12}) } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{10} \times \mathrm{dtanh}(u_1) \times 1 } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{10} \times \mathrm{dtanh}(u_1)} \\
\end{multline}
\]
\[
\begin{multline}
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{20}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_2}
\frac{\partial y_2}{\partial u_2} \frac{\partial u_2}{\partial w^1_{20}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial y_2}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ \times \frac{\partial}{\partial u_2}\mathrm{tanh}(u_2) \times
\frac{\partial}{\partial w^1_{20}}(x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22}) } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{11} \times \mathrm{dtanh}(u_2) \times x_0 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{21}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_2}
\frac{\partial y_2}{\partial u_2} \frac{\partial u_2}{\partial w^1_{21}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial y_2}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ \times \frac{\partial}{\partial u_2}\mathrm{tanh}(u_2) \times
\frac{\partial}{\partial w^1_{21}}(x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22}) } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{11} \times \mathrm{dtanh}(u_2) \times x_1 } \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^1_{22}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial y_2}
\frac{\partial y_2}{\partial u_2} \frac{\partial u_2}{\partial w^1_{22}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial y_2}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ \times \frac{\partial}{\partial u_2}\mathrm{tanh}(u_2) \times
\frac{\partial}{\partial w^1_{22}}(x_0 \times w^1_{20} + x_1 \times w^1_{21} + 1 \times w^1_{22}) } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{11} \times \mathrm{dtanh}(u_2) \times 1 } \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times w^2_{11} \times \mathrm{dtanh}(u_2)} \\
\end{multline}
\]
\[
\begin{multline}
\shoveleft{\displaystyle \frac{\partial E}{\partial w^2_{10}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w^2_{10}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial w^2_{10}}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times y_1} \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^2_{11}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w^2_{11}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial w^2_{11}}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times y_2} \\
\\
\shoveleft{\displaystyle \frac{\partial E}{\partial w^2_{12}} = \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w^2_{12}} } \\
\shoveleft{ = \displaystyle \frac{\partial}{\partial y}(x_3 – y)^2 \times \frac{\partial}{\partial u}\mathrm{tanh}(u)
\times \frac{\partial}{\partial w^2_{12}}(y_1 \times w^2_{10} + y_2 \times w^2_{11} + 1 \times w^2_{12})} \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u) \times 1} \\
\shoveleft{ = 2(y – x_3) \times \mathrm{dtanh}(u)}
\end{multline}
\]

さらに、先ほどのニューラルネットワークを呼び出した結果は以下の通りで、出力結果\(y\)は、入力値\(x_0=x_1=0\)または\(x_0=x_1=1\)の場合に\(0\)に近く、そうでない場合は\(1\)に近いことが確認できる。
import numpy as np
# 作成した入力データのフォワード&バックプロパゲーションを実行
input_data = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 0]])
for data in input_data:
onn = OrigNeuralNetwork(data)
print("*** 入力データ ***")
print(data)
print("*** 出力結果 ***")
onn.repeat_forward_back()
print(onn.get_y())
print()
また、先ほどのニューラルネットワークを呼び出した際のdwの最終結果は以下の通りで、それぞれ\(0\)に近づいていることが確認できる。
import numpy as np
# 作成した入力データのフォワード&バックプロパゲーションを実行
input_data = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 0]])
for data in input_data:
onn = OrigNeuralNetwork(data)
print("*** 入力データ ***")
print(data)
onn.repeat_forward_back()
print("*** 出力結果 ***")
print(onn.get_y())
# 小数点以下10桁まで+指数表記しない形式に設定後、dwの最終結果を出力
np.set_printoptions(precision=10, suppress=True)
print("*** dwの最終結果 ***")
print(onn.dw)
print()
要点まとめ
- 偏微分の計算ができれば、ニューラルネットワークの活性化関数に、tanh関数のようなシグモイド関数以外も利用することができる。





