これまでは、ニューラルネットワークを自前で作成していたが、TensorflowやKeras、PyTorchといった、深層学習のフレームワークも利用することができる。
今回は、自前で作成していたニューラルネットワークをKerasで作成してみたので、その手順とサンプルプログラムを共有する。
前提条件
下記記事のAnacondaをインストールしJupyter Notebookを利用できること。

やってみたこと
tensorflowパッケージのインストール
AnacondaでKerasを利用するには、Anacondaでtensorflowパッケージを使えるようにする必要がある。その手順は、以下の通り。
1) Windowsのスタートメニューから「Anaconda Prompt」を選択する。
2) 以下のように、「conda list -f tensorflow」コマンドを実行し、Anacondaにtensorflowパッケージが含まれていないことを確認する。
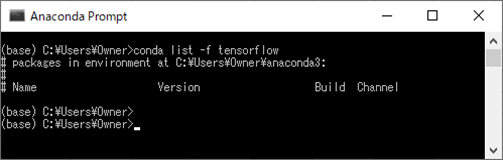
3)「pip install tensorflow」コマンドを実行し、tensorflowパッケージをインストールする。
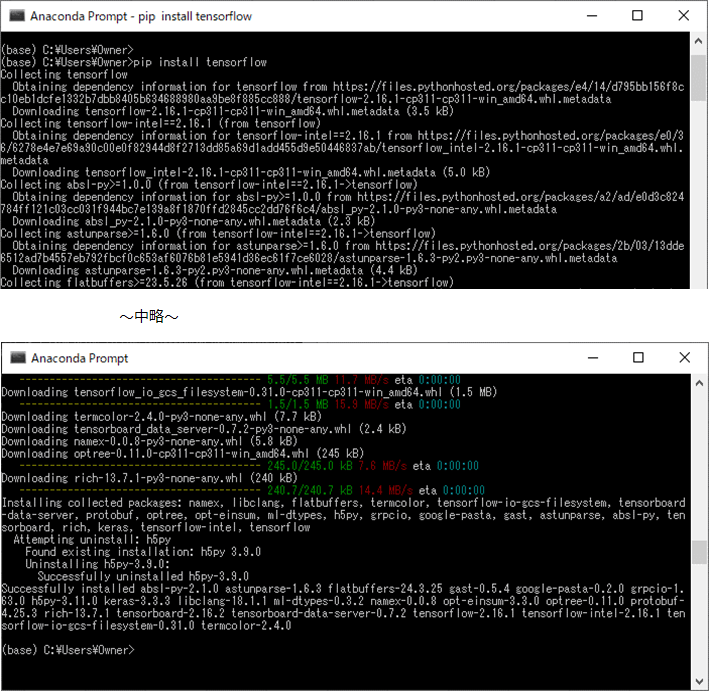
4)「conda list -f tensorflow」コマンドを再度実行し、Anacondaにtensorflowパッケージがインストールされたことを確認する。
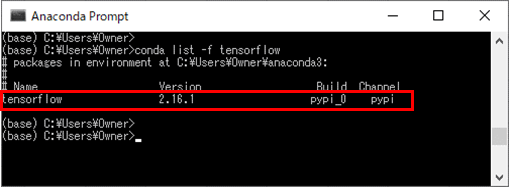

Kerasによるサンプルプログラムの作成と実行
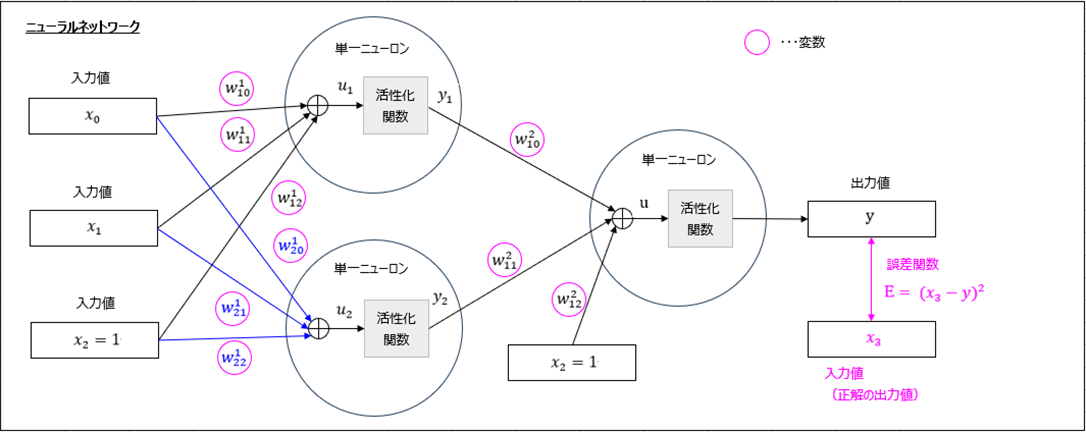
今回実装するニューラルネットワークの全体構成は、以下のようになる。
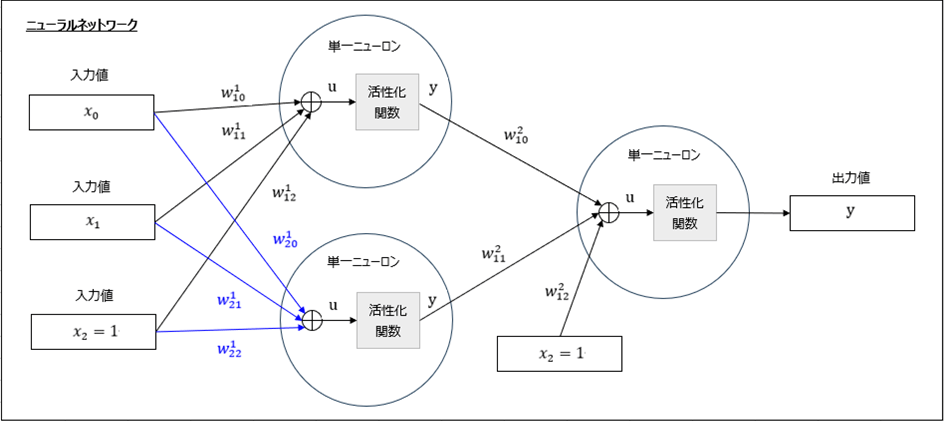
また、重み\(\boldsymbol w\)の最適解は、下図における誤差関数\(E=(x_3 – y)^2\)が最小となる箇所で、これは誤差関数を(桃枠の)各変数について偏微分した結果が\(0\)になる値となる。
上記を、行列を用いて自前で実装したサンプルプログラムは、以下の記事に記載している。

これと同等の内容を、Kerasで作成したサンプルプログラムの内容は、以下の通り。
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Activation, Dense
from tensorflow.keras.optimizers import SGD
import numpy as np
# Kerasでニューラルネットワークのモデルを作成する
model = Sequential()
# 入力値x_1, x_2を取り込む単一ニューロン(2個)を作成し、
# 活性化関数にシグモイド関数を指定
model.add(Dense(2, input_shape=(2,)))
model.add(Activation('sigmoid'))
# 出力値yを出力する単一ニューロン(1個)を作成し、
# 活性化関数にシグモイド関数を指定
model.add(Dense(1))
model.add(Activation('sigmoid'))
# モデルをコンパイル
# その際、損失(誤差)関数(loss)、最適化関数(optimizer)、評価関数(metrics)を指定
#
# 損失(誤差)関数(loss)に平均二乗誤差(mse)を指定
# 最適化関数(optimizer)に確率的勾配(最急)降下法(SGD)を指定
# learning_rate(デフォルト値:0.01)に学習率ηを指定
# momentum=0.0、nesterov=Falseを指定することで、勾配(最急)降下法になる
# 評価関数(metrics)に正解率(accuracy)を指定
#
sgd = SGD(learning_rate=0.1, momentum=0.0, decay=0.0, nesterov=False)
model.compile(loss='mse', optimizer=sgd, metrics=['accuracy'])
# 入力データ、正解データを読み込む
input_data_x = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
input_data_x3 = np.array([[0], [1], [1], [0]])
# 読み込んだデータを用いて、モデルの学習を行う
# 繰り返し回数はepochsで指定
model.fit(input_data_x, input_data_x3, epochs=10000)
# 学習済モデルを用いた検証を行う
input_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
print("*** 入力データ ***")
print(input_data)
print("*** 出力結果 ***")
results = model.predict(input_data)
print(results)なお、確率的勾配(最急)降下法(SGD)のクラスは、以下のサイトを参考にして設定している。
出所:SGDクラスの説明
また、損失(誤差)関数(loss)、最適化関数(optimizer)については、以下のサイトを参照のこと。
●損失(誤差)関数
https://qiita.com/Hatomugi/items/d00c1a7df07e0e3925a8
●最適化関数
https://qiita.com/tokkuman/items/1944c00415d129ca0ee9
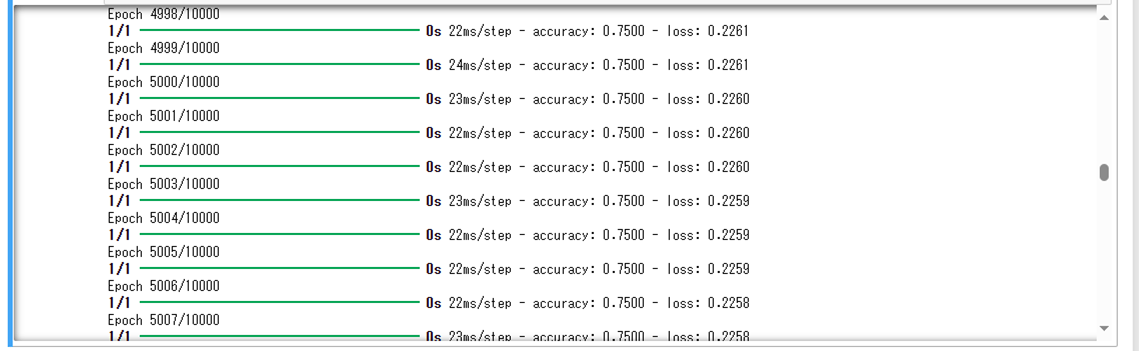
上記サンプルプログラムの最終実行結果は以下の通りで、出力結果\(y\)は、入力値\(x_0=x_1=0\)または\(x_0=x_1=1\)の場合に\(0\)に近く、そうでない場合は\(1\)に近いことが確認できる。
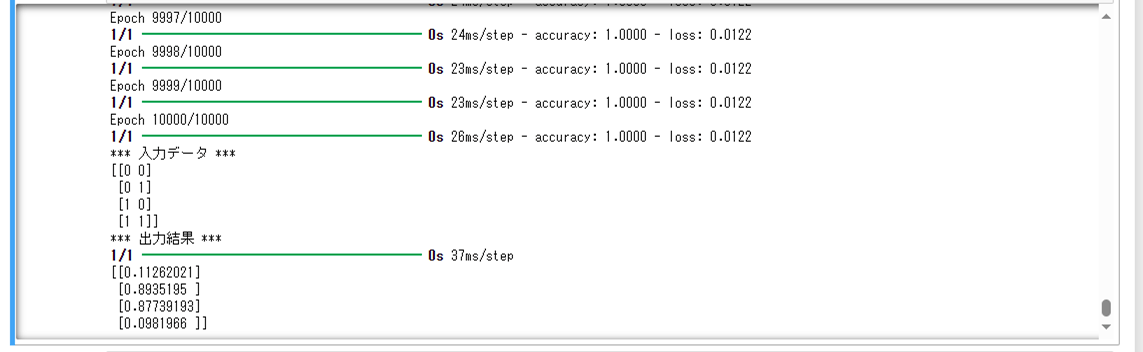
また、上記サンプルプログラムを実行した場合の途中の結果は、以下の通り。
要点まとめ
- 深層学習のフレームワークには、TensorflowやKeras、PyTorchがある。
- Kerasを利用すると、ニューラルネットワークのモデル構築や学習を簡単に行うことができる。