以下のように、損失(誤差)関数で「交差エントロピー誤差」を利用し、活性化関数に「ReLU関数」「ソフトマックス関数」を利用した分類モデルを考える。
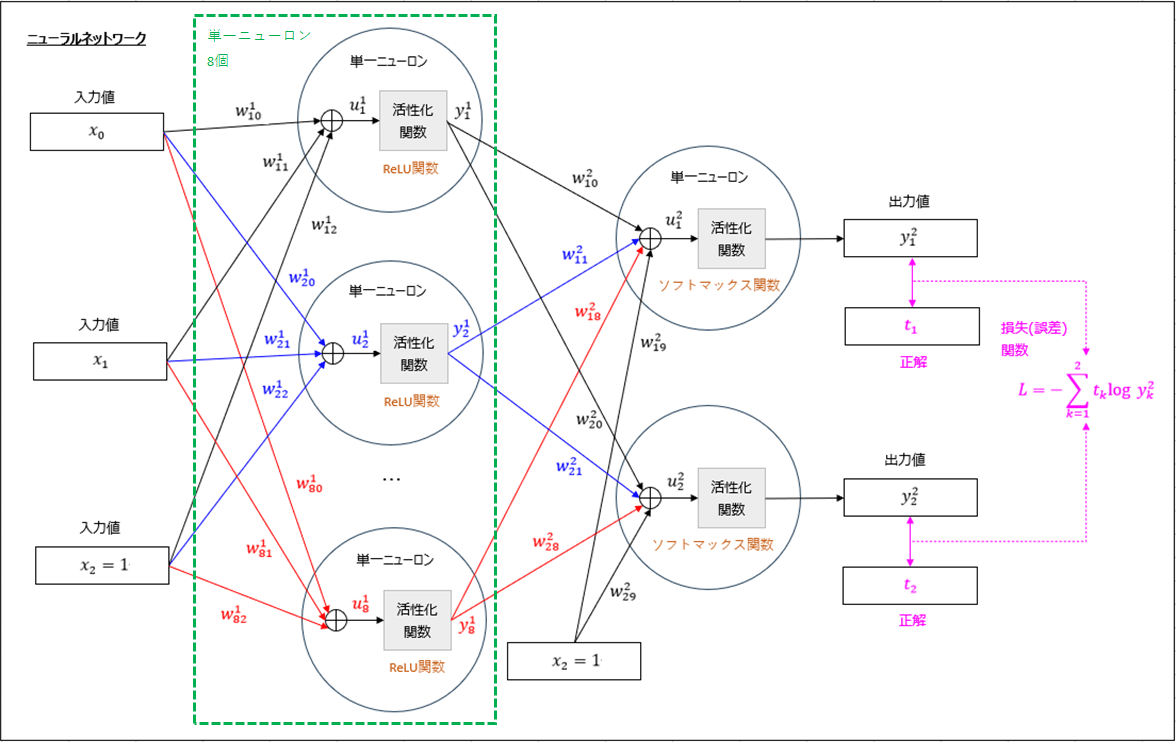
上図において、入力値\((x_0, x_1) = (0, 0), (0, 1), (1, 0), (1, 1)\)、
正解値\((t_1, t_2) = (1, 0), (0, 1), (0, 1), (1, 0)\)とする。
上記モデルをKerasで実装した結果は、以下の通り。
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Activation, Dense
from tensorflow.keras.optimizers import SGD
import numpy as np
# Kerasでニューラルネットワークのモデルを作成する
model = Sequential()
# 入力値x_1, x_2を取り込む単一ニューロン(8個)を作成し、
# 活性化関数にReLU関数を指定
model.add(Dense(8, input_shape=(2,)))
model.add(Activation('relu'))
# 出力値yを出力する単一ニューロン(2個)を作成し、
# 活性化関数にソフトマックス関数を指定
model.add(Dense(2))
model.add(Activation('softmax'))
# モデルをコンパイル
# その際、損失(誤差)関数(loss)、最適化関数(optimizer)、評価関数(metrics)を指定
#
# 損失(誤差)関数(loss)に多クラス分類(CategoricalCrossentropy)を指定
# 最適化関数(optimizer)に確率的勾配(最急)降下法(SGD)を指定
# learning_rate(デフォルト値:0.01)に学習率ηを指定
# momentum=0.0、nesterov=Falseを指定することで、勾配(最急)降下法になる
# 評価関数(metrics)に正解率(accuracy)を指定
#
sgd = SGD(learning_rate=0.1, momentum=0.0, decay=0.0, nesterov=False)
model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy'])
# 入力データ、正解データを読み込む
input_data_x = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
input_data_x3 = np.array([[1, 0], [0, 1], [0, 1], [1, 0]])
# 読み込んだデータを用いて、モデルの学習を行う
# 繰り返し回数はepochsで指定
model.fit(input_data_x, input_data_x3, epochs=1000)
# 学習済モデルを用いた検証を行う
input_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
print("*** 入力データ ***")
print(input_data)
print("*** 出力結果 ***")
results = model.predict(input_data)
print(results)

「MiniTool Partition Wizard」はパーティション分割・統合・バックアップ・チェックを直感的に行える便利ツールだったハードディスクの記憶領域を論理的に分割し、分割された個々の領域のことを、パーティションといいます。 例えば、以下の図の場合、C/D...
また、上記モデルを独自に実装した結果は、以下の通り。
import numpy as np
# 単一ニューロン(活性化関数:ReLU)
class OrigNeuronRelu:
# クラス変数
eta = 0.1 # 学習率η
# 変数の初期化
def __init__(self):
# 入力データ(変数x)
self.x = np.array([])
# 入力データ(重みw)
self.w = np.array([])
# 出力データ(活性化関数の変換前)
self.u = 0
# 出力データ
self.y = 0
# 入力データ(変数x、重みw:いずれもNumpy配列)の設定
def set_input_data(self, x, w):
if self.__input_check(x, 2) and self.__input_check(w, 3):
self.x = x
self.w = w
# フォワードプロパゲーションで行列の乗算ができるよう、
# xの末尾に1を追加
self.x = np.append(self.x, 1)
else:
print("OrigNeuronRelu set_input_data : 引数の指定方法が誤っています")
# フォワードプロパゲーションで出力変数を設定
def forward(self):
if self.__input_check(self.x, 3) and self.__input_check(self.w, 3):
self.u = np.dot(self.x, self.w)
self.y = self.__relu(self.u)
# バックプロパゲーションで入力データ(重みw)を変更
def back(self, dw):
if self.__input_check(dw, 3):
# 引数の偏微分を利用して、最急降下法により、重みwの値を更新する
self.w = self.w - OrigNeuronRelu.eta * dw
# 出力データyを返却
def get_y(self):
return self.y
# 重みwを返却
def get_w(self):
return self.w
# 入力データの型・長さをチェック
def __input_check(self, data, size):
if isinstance(data, np.ndarray) and len(data) == size:
if np.issubdtype(data.dtype, float) or np.issubdtype(data.dtype, int):
return True
return False
return False
# ReLU関数による変換
def __relu(self, data):
return np.where(data < 0, 0, data)import numpy as np
# 単一ニューロン(活性化関数:softmax)
class OrigNeuronSoftmax:
# クラス変数
eta = 0.1 # 学習率η
# 変数の初期化
def __init__(self):
# 入力データ(変数x)
self.x = np.array([])
# 入力データ(重みw)
self.w = np.array([])
# 出力データ(活性化関数の変換前)
self.u = 0
# 出力データ
self.y = 0
# 入力データ(変数x、重みw:いずれもNumpy配列)の設定
def set_input_data(self, x, w):
if self.__input_check(x, 9) and self.__input_check(w, 9):
self.x = x
self.w = w
else:
print("OrigNeuronSoftmax set_input_data : 引数の指定方法が誤っています")
# フォワードプロパゲーションで出力変数を設定
# 出力関数yはニューラルネットワーク側で設定
def forward(self):
if self.__input_check(self.x, 9) and self.__input_check(self.w, 9):
self.u = np.dot(self.x, self.w)
# バックプロパゲーションで入力データ(重みw)を変更
def back(self, dw):
if self.__input_check(dw, 9):
# 引数の偏微分を利用して、最急降下法により、重みwの値を更新する
self.w = self.w - OrigNeuronSoftmax.eta * dw
# 出力データyを返却
def get_y(self):
return self.y
# 出力データyを設定
def set_y(self, y):
self.y = y
# 出力データuを返却
def get_u(self):
return self.u
# 重みwを返却
def get_w(self):
return self.w
# 入力データの型・長さをチェック
def __input_check(self, data, size):
if isinstance(data, np.ndarray) and len(data) == size:
if np.issubdtype(data.dtype, float) or np.issubdtype(data.dtype, int):
return True
return False
return Falseimport numpy as np
# ニューラルネットワーク
class OrigNeuralNetwork:
# クラス変数
repeat_num = 1000 # 最急降下法の繰り返し回数
# 変数の初期化
# 変数x,t、重みw1,w2、重みの微分dw1,dw2:いずれもNumpy配列 の設定
# ニューロンの生成と初期値の代入
def __init__(self, x, t):
if self.__input_check(x, 2) and self.__input_check(t, 2):
self.x = x # 入力値x_0,x_1
self.t = t # 入力値t_0,t_1(正解値)
self.w1 = np.ones((8, 3), dtype="float64") # 重みw1
self.dw1 = np.ones((8, 3), dtype="float64") # 重みの微分dw1
self.w2 = np.ones((2, 9), dtype="float64") # 重みw2
self.dw2 = np.ones((2, 9), dtype="float64") # 重みの微分dw2
# ニューロンの生成と初期値の代入
self.on1 = []
self.on2 = []
# 活性化関数がReLU関数である単一ニューロン(8個)
for num in range(0, 8):
self.on1.append(OrigNeuronRelu())
self.on1[num].set_input_data(self.x, self.w1[num])
# 活性化関数がソフトマックス関数である単一ニューロン(2個)
for num in range(0, 2):
self.on2.append(OrigNeuronSoftmax())
self.on2[num].set_input_data(
np.array([self.on1[0].get_y(), self.on1[1].get_y()
, self.on1[2].get_y(), self.on1[3].get_y()
, self.on1[4].get_y(), self.on1[5].get_y()
, self.on1[6].get_y(), self.on1[7].get_y()
, 1.0]), self.w2[num])
else:
self.x = np.array([])
print("OrigNeuralNetwork set_input_data : 引数の指定方法が誤っています")
# フォワードプロパゲーションとバックプロパゲーションを繰り返す
def repeat_forward_back(self):
for num in range(OrigNeuralNetwork.repeat_num):
self.forward()
self.back()
# フォワードプロパゲーションで出力変数を設定
def forward(self):
if self.__input_check(self.x, 2):
# 重みw1を更新
for num in range(0, 8):
self.on1[num].forward()
# 重みw2を更新
for num in range(0, 2):
self.on2[num].forward()
self.on2[0].set_y(self.__softmax_list(
[self.on2[0].get_u(), self.on2[1].get_u()])[0])
self.on2[1].set_y(self.__softmax_list(
[self.on2[0].get_u(), self.on2[1].get_u()])[1])
# バックプロパゲーションで重み、出力変数を変更
def back(self):
### 重みの微分dw2、重みw2を更新
# 誤差関数をu^2_1、u^2_2で偏微分した結果を計算
self.dw2[0][8] = self.on2[0].get_y() - self.t[0]
self.dw2[1][8] = self.on2[1].get_y() - self.t[1]
# 誤差関数をw^2_numで偏微分した結果を計算
for num in range(0, 8):
self.dw2[0][num] = self.dw2[0][8] * self.on1[num].get_y()
self.dw2[1][num] = self.dw2[1][8] * self.on1[num].get_y()
# 重みの微分dw2、重みw2を更新
for num in range(0, 2):
self.on2[num].back(self.dw2[num])
self.w2[num] = self.on2[num].get_y()
### 重みの微分dw1、重みw1を更新
for num in range(0, 8):
# 誤差関数をy^1_numで偏微分した結果を計算
self.dw1_y = (self.on2[0].get_y() - self.t[0]) * self.dw2[0][num] \
+ (self.on2[1].get_y() - self.t[1]) * self.dw2[1][num]
# 誤差関数をw^1_numで偏微分した結果を計算
self.dw1[num][2] = self.dw1_y * self.__d_relu(self.on2[0].get_u())
self.dw1[num][0] = self.dw1[num][2] * self.x[0]
self.dw1[num][1] = self.dw1[num][2] * self.x[1]
# 重みの微分dw1、重みw1を更新
self.on1[num].back(self.dw1[num])
self.w1[num] = self.on1[num].get_y()
# 出力データを返却
def get_y(self):
if self.__input_check(self.x, 2):
# 出力結果y^2_1、y^2_2を返却
return np.array([self.on2[0].get_y(), self.on2[1].get_y()])
else:
return None
# 入力データの型・長さをチェック
def __input_check(self, data, size):
if isinstance(data, np.ndarray) and len(data) == size:
if np.issubdtype(data.dtype, float) or np.issubdtype(data.dtype, int):
return True
return False
return False
# ソフトマックス関数の値
def __softmax_list(self, data_list):
after_data_list = data_list - np.max(data_list)
return np.exp(after_data_list) / np.sum(np.exp(after_data_list))
# ReLU関数の微分の値
def __d_relu(self, u):
return np.where(u < 0, 0, 1)なお、上記のバックプロパゲーションの実装は、以下のサイトに記載の知識を組み合わせている。

ニューラルネットワークの誤差関数の微分を計算してみた 以下の記事で、ニューラルネットワークのフォワードプロパゲーションによる出力値\(y\)を算出してきたが、その際、重み\(\bolds...

交差エントロピー誤差とそれを利用した微分を計算してみた 入力値を\(y=(y_1,y_2,\ldots,y_K)\)、正解値を\(t=(t_1,t_2,\ldots,t_K)\)とした場合...

ReLU関数とその微分をグラフ化してみた 以下の式で表現される関数をReLU関数といい、ディープラーニングの活性化関数の1つとして利用される。
\[
\begin{eqn...
import numpy as np
# 入力データ、正解データ
input_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
correct_data = np.array([[1, 0], [0, 1], [0, 1], [1, 0]])
# 作成した入力データのフォワード&バックプロパゲーションを実行
for num in range(0, 4):
print("*** 入力データ ***")
print(input_data[num])
print("*** 正解データ ***")
print(correct_data[num])
onn = OrigNeuralNetwork(input_data[num], correct_data[num])
onn.repeat_forward_back()
print("*** 出力結果 ***")
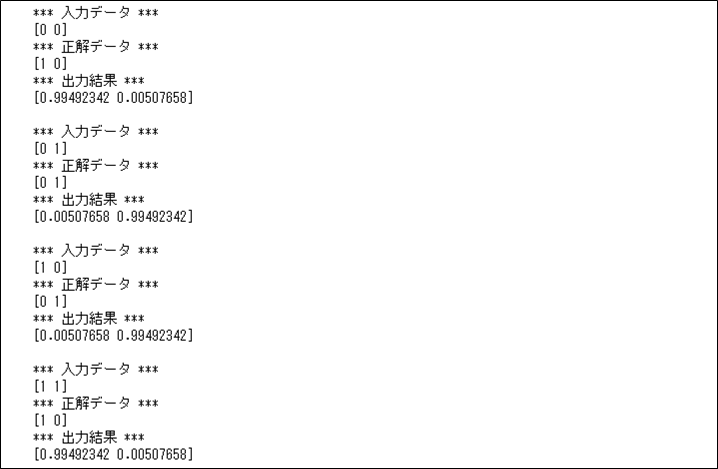
print(onn.get_y())
print()上記「分類モデルのニューラルネットワークの呼び出し」を実行した結果は以下の通りで、出力結果が正解データに近くなっていることが確認できる。
要点まとめ
- ニューラルネットワークの分類モデルでは、損失(誤差)関数で「交差エントロピー誤差」を、活性化関数に「ソフトマックス関数」を利用することが多い。





