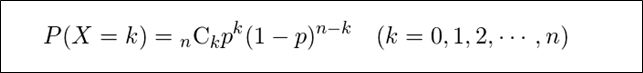互いに独立な\(n\)回のベルヌーイ試行(=コインの裏表のように、何かを行ったときに起こる結果が2つしかない試行)を行うときにちょうど\(k\)回成功する確率は、以下の式で表せる。
出所:統計WEB_二項分布
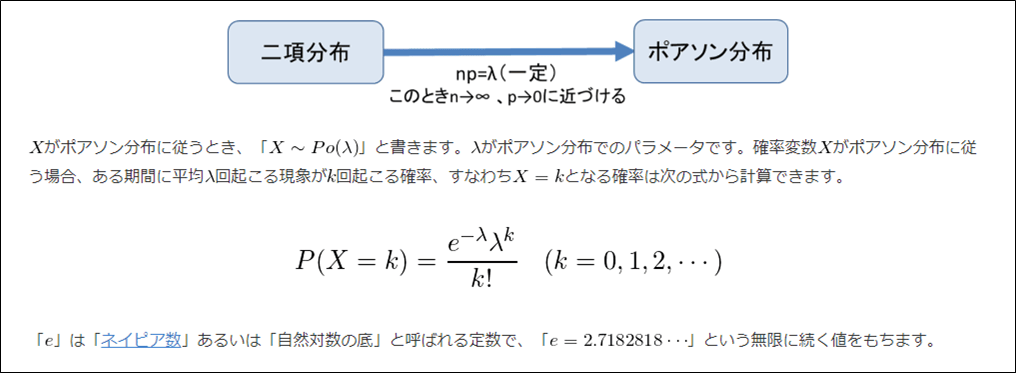
上記式で定義される二項分布は、\(n\)が十分大きい場合に確率の計算が難しくなるが、以下のポアソン分布に近似して計算することができる。
出所:統計WEB_ポアソン分布
例えば、ポアソン分布で\(λ=2\)の場合の確率を表形式でまとめると、以下のようになる。
| \(k\) | 確率 |
|---|---|
| \(0\) | \(P(X=0)=\displaystyle \frac{e^{-2}2^0}{0!}=e^{-2}≒0.135\) |
| \(1\) | \(P(X=1)=\displaystyle \frac{e^{-2}2^1}{1!}=2e^{-2}≒0.271\) |
| \(2\) | \(P(X=2)=\displaystyle \frac{e^{-2}2^2}{2!}=2e^{-2}≒0.271\) |
| \(3\) | \(P(X=3)=\displaystyle \frac{e^{-2}2^3}{3!}=\frac{4}{3}e^{-2}≒0.180\) |
| \(4\) | \(P(X=4)=\displaystyle \frac{e^{-2}2^4}{4!}=\frac{2}{3}e^{-2}≒0.090\) |
| \(5\) | \(P(X=5)=\displaystyle \frac{e^{-2}2^5}{5!}=\frac{4}{15}e^{-2}≒0.036\) |
| \(6\) | \(P(X=6)=\displaystyle \frac{e^{-2}2^6}{6!}=\frac{4}{45}e^{-2}≒0.012\) |
| \(7\) | \(P(X=7)=\displaystyle \frac{e^{-2}2^7}{7!}=\frac{8}{315}e^{-2}≒0.0034\) |
| \(8\) | \(P(X=8)=\displaystyle \frac{e^{-2}2^8}{8!}=\frac{2}{315}e^{-2}≒0.00086\) |
| \(9\) | \(P(X=9)=\displaystyle \frac{e^{-2}2^9}{9!}=\frac{4}{2835}e^{-2}≒0.00019\) |
また、この確率を計算しグラフにまとめた場合の、ソースコードと実行結果は、以下のようになる。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# n!(=1*2*・・・*n、nの階乗)を計算
def factorial(n):
ret = 1
for num in range(1, n + 1):
ret = ret * num
return ret
# ポアソン分布の計算
def poisson(k, lmd):
return (np.e**(lmd*(-1)) * lmd**k) / factorial(k)
# ポアソン分布でλ=2の場合の確率をそれぞれ計算
lmd = 2
p_list = list()
for num in range(0, 10):
p_list.append(poisson(num, lmd))
print("*** ポアソン分布でλ=2の場合の確率をそれぞれ計算した結果 ***")
print("k=0の確率 = " + str(p_list[0]))
print("k=1の確率 = " + str(p_list[1]))
print("k=2の確率 = " + str(p_list[2]))
print("k=3の確率 = " + str(p_list[3]))
print("k=4の確率 = " + str(p_list[4]))
print("k=5の確率 = " + str(p_list[5]))
print("k=6の確率 = " + str(p_list[6]))
print("k=7の確率 = " + str(p_list[7]))
print("k=8の確率 = " + str(p_list[8]))
print("k=9の確率 = " + str(p_list[9]))
# ポアソン分布でλ=2の場合の確率を棒グラフで描画
k_list_array = np.arange(10)
p_list_array = np.array(p_list)
plt.bar(k_list_array, p_list_array)
plt.title("poisson graph")
plt.xlabel("k", size=14)
plt.ylabel("p", size=14)
plt.show()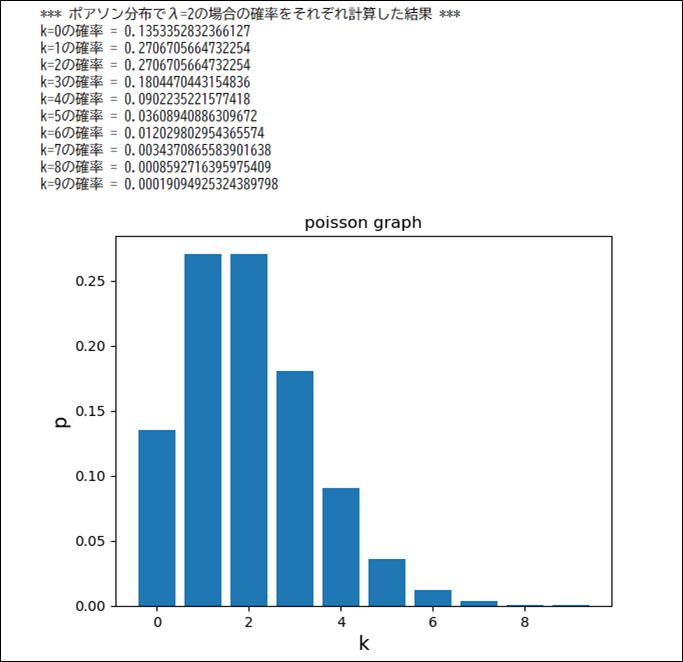
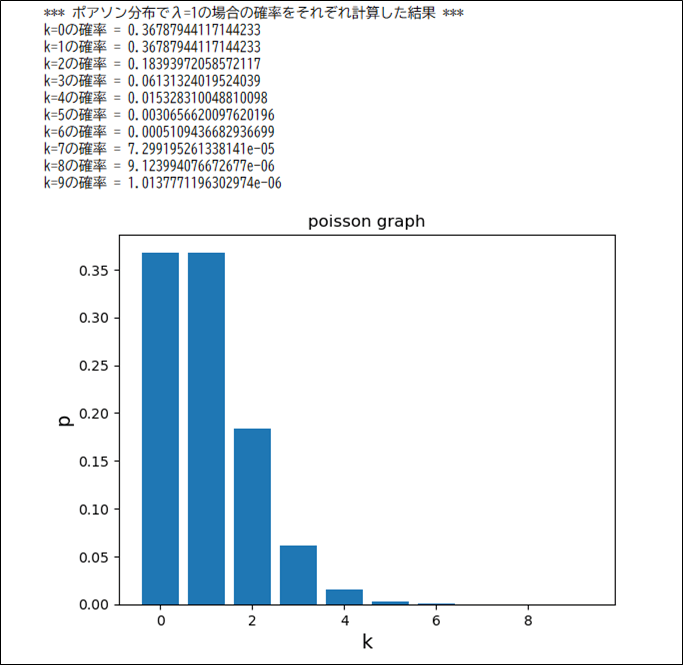
上記プログラムで、\(λ=1、λ=5、λ=9\)とした場合の実行結果は、それぞれ以下の通りで、\(λ\)に近い確率\(k\)が大きくなっていることが確認できる。
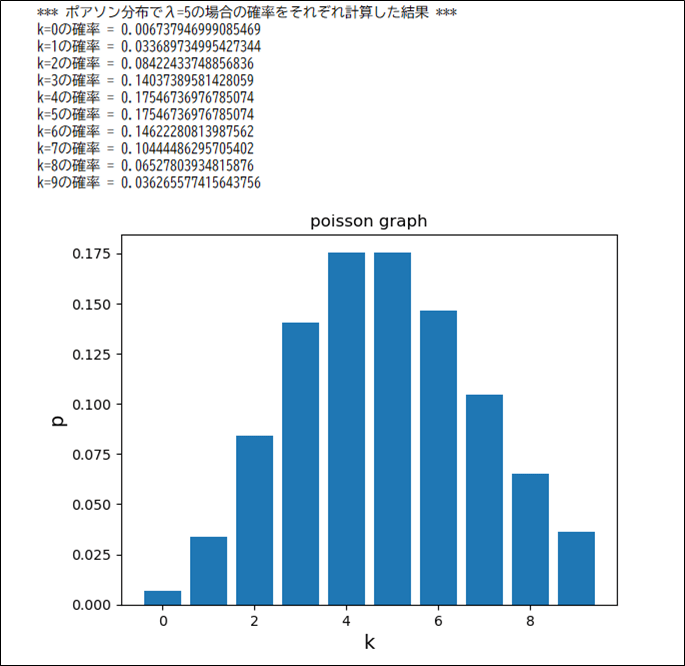
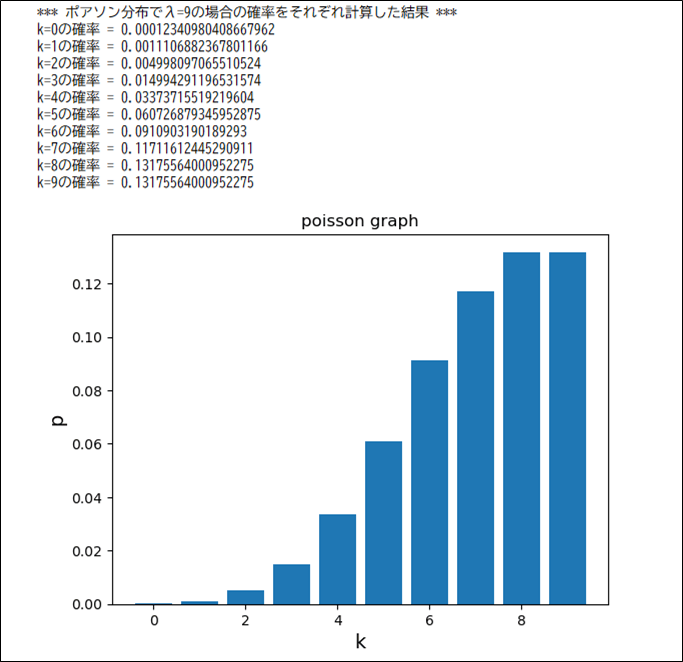

さらに、二項分布の確率変数\(P(X=k)={}_n \mathrm{ C }_kp^k(1-p)^{n-k} (k=0,1,2,\cdots,n)\)において、\(np=λ\)(一定)・\(n→∞、p→0\)に近づけると、ポアソン分布の確率変数\(P(X=k)=\displaystyle \frac{e^{-λ}λ^k}{k!} (k=0,1,2,\cdots)\)が導けることは、以下のように示すことができる。
\[
\begin{eqnarray}
\displaystyle \lim_{n \to \infty} {}_n \mathrm{ C }_kp^k(1-p)^{n-k}
&=& \displaystyle \lim_{n \to \infty} \frac{n!}{(n-k)!k!} \left( \frac{λ}{n} \right)^k \left( 1 – \frac{λ}{n} \right)^{n-k} \\
&=& \displaystyle \lim_{n \to \infty} \frac{n(n-1)(n-2) \cdots (n-k+1)}{k!} \times \frac{λ^k}{n^k} \times \left( 1 – \frac{λ}{n} \right)^{n-k} \\
&=& \displaystyle \lim_{n \to \infty} \frac{n(n-1)(n-2) \cdots (n-k+1)}{n^k} \times \frac{λ^k}{k!} \times \left( 1 – \frac{λ}{n} \right)^n \times \left( 1 – \frac{λ}{n} \right)^{-k} \\
&=& \displaystyle \lim_{n \to \infty} \frac{n}{n} \frac{n-1}{n} \frac{n-2}{n} \cdots \frac{n-k+1}{n}
\times \frac{λ^k}{k!} \times \left\{ 1 + \left( \frac{1}{- \displaystyle \frac{n}{λ}} \right) \right\}^{- \displaystyle \frac{n}{λ} \times (-λ)}
\times \left( 1 – \frac{λ}{n} \right)^{-k} \\
&=& 1 \times 1 \times 1 \times \cdots \times 1 \times \frac{λ^k}{k!} \times e^{-λ} \times 1 = \frac{e^{-λ}λ^k}{k!}
\end{eqnarray}
\]
なお、上記計算では、ネイピア数\(e\)の定義式\(e=\displaystyle \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n \)を利用している。
また、ポアソン分布の期待値\(E(X)\)と分散\(V(X)\)は、二項分布において\(np=λ\)(一定)・\(n→∞、p→0\)に近づけることで\(1-p→1\)に近づくため、以下のように計算できる。
\[
\begin{eqnarray}
E(X) &=& np=n \times \displaystyle \frac{λ}{n}=λ \\
V(X) &=& np(1-p)=np \times 1=np=n \times \displaystyle \frac{λ}{n}=λ
\end{eqnarray}
\]
要点まとめ
- 二項分布で\(n\)が十分大きい場合、確率の計算が難しくなるが、ポアソン分布に近似して計算することができる。
- ポアソン分布の確率変数は、二項分布において\(np=λ\)とすると、\(P(X=k)=\displaystyle \frac{e^{-λ}λ^k}{k!} (k=0,1,2,\cdots)\)と表せる。
- ポアソン分布において、期待値\(E(X)=λ\)、分散\(V(X)=λ\)となる。