データの分布を表現する手法に、度数分布表・ヒストグラム・箱ひげ図等があり、これらはPythonのMatplotlibライブラリを利用して作成することができる。
今回は、度数分布表・ヒストグラム・箱ひげ図をPythonで作成してみたので、そのサンプルプログラムを共有する。
なお、度数分布表・ヒストグラムについては、以下のサイトを参照のこと。
https://taimuoreganoblog.com/home/math/frequency-distribution-table-histogram/
また、箱ひげ図や、そこで利用する四分位数については、以下のサイトを参照のこと。
https://avilen.co.jp/personal/knowledge-article/boxplot/
前提条件
下記記事のAnacondaをインストールしJupyter Notebookを利用できること

乱数の生成
numpy.randomモジュールを利用すると、乱数の生成ができる。0~99までの乱数を20個作成し表示するソースコードの内容は、以下の通り。
import numpy as np # 0~99までの乱数を20個作成し、表示する x = np.random.randint(0,100,20) print(x)
上記ソースコードを実行した結果(一例)は、以下の通り。乱数なので、実行結果は毎回変わる。
![]()
度数分布表・ヒストグラム・箱ひげ図の表示
度数分布表の表示は、例えば以下のサイトの「Frequency_Distribution」関数を利用できる。
https://qiita.com/TakuTaku36/items/91032625e482f2ae6e18
上記サイトの「Frequency_Distribution」関数を利用し、0~99までの乱数を1000個作成し、度数分布表を表示するソースコードと実行結果は、以下の通り。
import numpy as np
import pandas as pd
def Frequency_Distribution(data, class_width=None):
data = np.asarray(data)
if class_width is None:
class_size = int(np.log2(data.size).round()) + 1
class_width = round((data.max() - data.min()) / class_size)
bins = np.arange(0, data.max()+class_width+1, class_width)
hist = np.histogram(data, bins)[0]
cumsum = hist.cumsum()
return pd.DataFrame({'階級値': (bins[1:] + bins[:-1]) / 2,
'度数': hist,
'累積度数': cumsum,
'相対度数': hist / cumsum[-1],
'累積相対度数': cumsum / cumsum[-1]},
index=pd.Index([f'{bins[i]}以上{bins[i+1]}未満'
for i in range(hist.size)],
name='階級'))
# 0~99までの乱数を1000個作成し、度数分布表を表示する
x = np.random.randint(0, 100, 1000)
Frequency_Distribution(x, 10)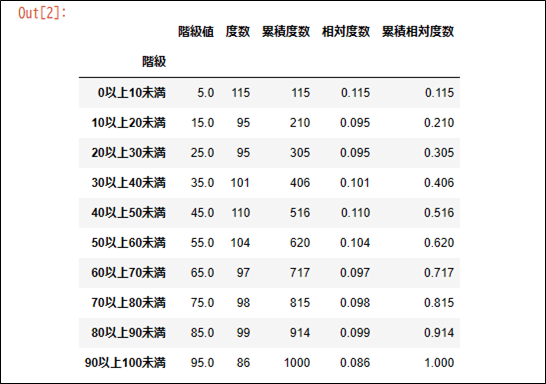
また、この度数分布表から、ヒストグラム・累積分布図を表示するソースコードと実行結果は、以下の通り。
%matplotlib inline
import matplotlib.pyplot as plt
# グラフを2つ並べて表示するための領域を定義
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
# 先ほど作成した乱数xのヒストグラムを表示する
ax1.hist(x, bins=10)
ax1.set_title("histogram")
# 先ほど作成した乱数xの累積分布図を表示する
ax2.hist(x, bins=10, cumulative=True)
ax2.set_title("cumulative distribution")
fig.tight_layout()
plt.show()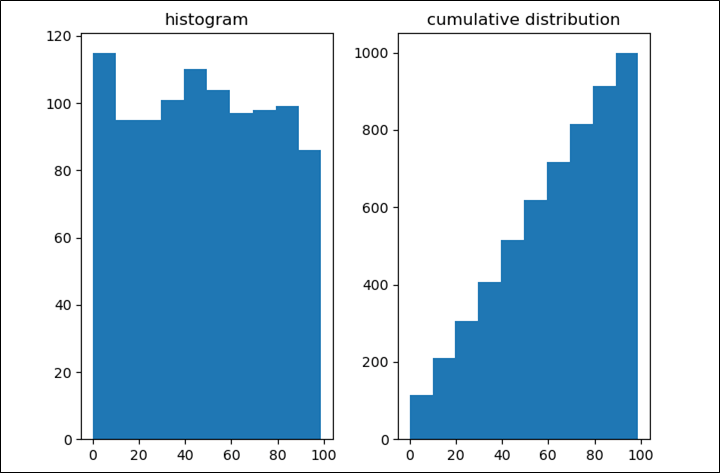
さらに、この度数分布表から、四分位数を計算し箱ひげ図を表示するソースコードと実行結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# 先ほど作成した乱数xの各四分位数を表示する
# 第一四分位数
q1 = np.percentile(x, 25)
# 第二四分位数(中央値と同じ)
q2 = np.percentile(x, 50)
# 第三四分位数
q3 = np.percentile(x, 75)
# 四分位範囲
iqr = q3 - q1
# 計算した各値を表示
print("第一四分位数:", q1)
print("第二四分位数(中央値):", q2)
print("第一四分位数:", q3)
print("四分位範囲:", iqr)
# 先ほど作成した乱数xの箱ひげ図を表示する
plt.boxplot(x)
plt.show()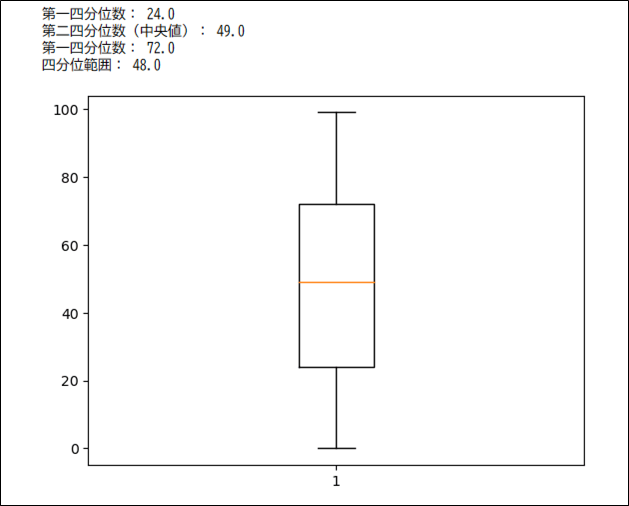
要点まとめ
- データの分布を表現できる度数分布表・ヒストグラム・箱ひげ図は、PythonのMatplotlibライブラリで作成することができる。





