重回帰分析を行うデータを読み込んでみた

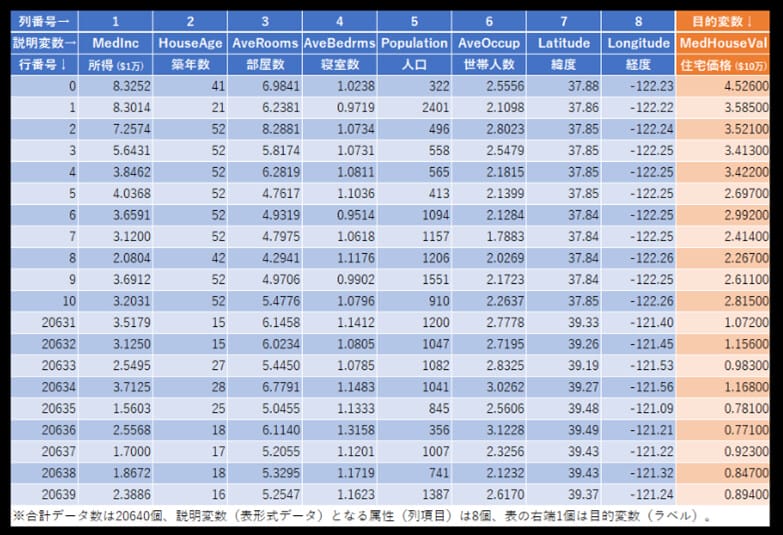
以下の「カリフォルニアの住宅価格データ」で、所得・築年数・部屋数・寝室数・人口・世帯人数・緯度・経度を元に、住宅価格を決めるモデルを考える。

出所：California Housingデータセットの内容例

上記データは、代表的な機械学習フレームワークであるscikit-learnのデータセットに含まれているため、これをPythonで読み込むことができる。その結果は、以下の通り。

上記結果を確認すると、「先頭5件のデータ」が分かりにくいため、表示形式を変更して表示する。その結果は、以下の通り。

「Envader」はLinuxコマンドやDatabase SQL等のスキルを、環境構築不要で習得できる学習サイトだった「Envader」は、ITエンジニアとしてよく使うLinuxコマンドやDatabase SQL等のスキルを、解説を読んだ上で、問題を解き...

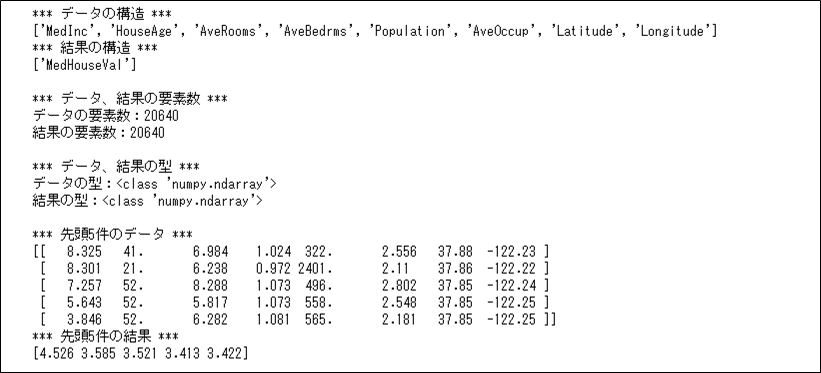
例えば先頭行のデータの場合、\(x_{11}\)(MedInc(所得))=\(8.325\)、\(x_{12}\)(HouseAge(築年数))=\(41.0\)、\(x_{13}\)(AveRooms(部屋数))=\(6.984\)、\(x_{14}\)(AveBedrms(寝室数))=\(1.024\)、\(x_{15}\)(Population(人口))=\(322.0\)、\(x_{16}\)(AveOccup(世帯人数))=\(2.556\)、\(x_{17}\)(Latitude(緯度))=\(37.88\)、\(x_{18}\)(Longitude(経度))=\(-122.23\)で、\(y_{1}\)(MedHouseVal(住宅価格))=\(4.526\)と読み取れる。

ここで、上記\(x_{11}\)～\(x_{18}\)を利用し、各係数の重みを\(w_{1}\)～\(w_{8}\)、バイアスを\(b\)とすると、\(y_{1}\)(MedHouseVal(住宅価格))の予測値\(\hat y_{1}\)は、以下の重回帰式で表現できる。
\[
\begin{eqnarray}
\hat y_{1} &=& w_{1}x_{11} + w_{2}x_{12} + w_{3}x_{13} + w_{4}x_{14} + w_{5}x_{15} + w_{6}x_{16} + w_{7}x_{17} + w_{8}x_{18} + b \\
&=& w_{1}x_{11} + w_{2}x_{12} + \ldots + w_{8}x_{18} + b
\end{eqnarray}
\]

また、\(b = w_{0} \times 1 = w_{0}x_{10}\) と定義すると、以下のように式変形できる。
\[
\begin{eqnarray}
\hat y_{1} &=& w_{1}x_{11} + w_{2}x_{12} + \ldots + w_{8}x_{18} + w_{0}x_{10} \\
&=& w_{0}x_{10} + w_{1}x_{11} + w_{2}x_{12} + \ldots + w_{8}x_{18} \\
&=& x_{10}w_{0} + x_{11}w_{1} + x_{12}w_{2} + \ldots + x_{18}w_{8} \\
&=& \begin{pmatrix} x_{10} & x_{11} & x_{12} & \ldots & x_{18} \end{pmatrix} \begin{pmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{8} \end{pmatrix}
= {}^t \! \boldsymbol x \boldsymbol w
\end{eqnarray}
\]

先頭5件分のデータから、上記式の( \(x_{i0}　x_{i1}　x_{i2}　･･･　x_{i8}\) ) (\(i=1～5\)、\(x_{i0}=1\))の部分を抜き出した結果は、以下の通り。

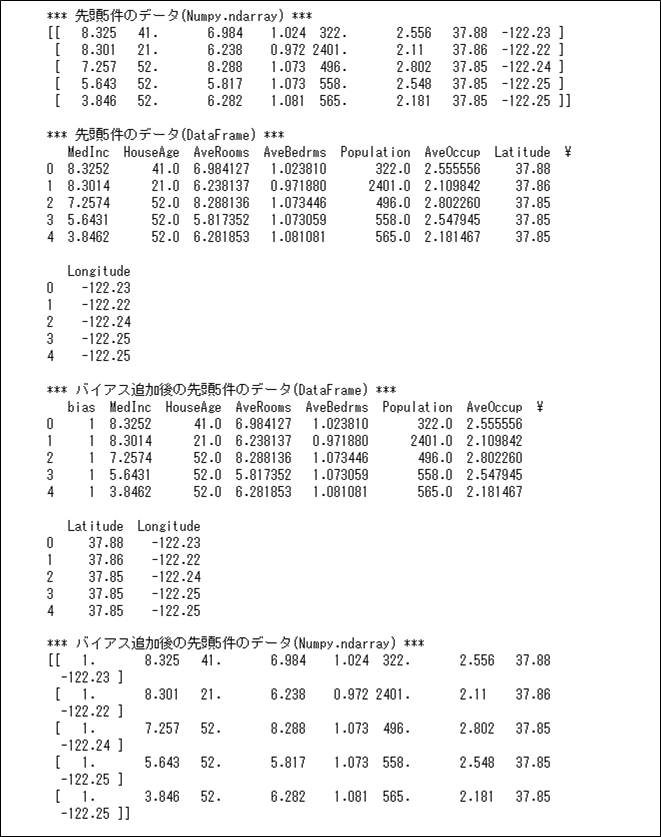
要点まとめ

• カリフォルニアの住宅価格データは、代表的な機械学習フレームワークであるscikit-learnのデータセットに含まれているため、これをPythonで読み込むことができる。