機械学習

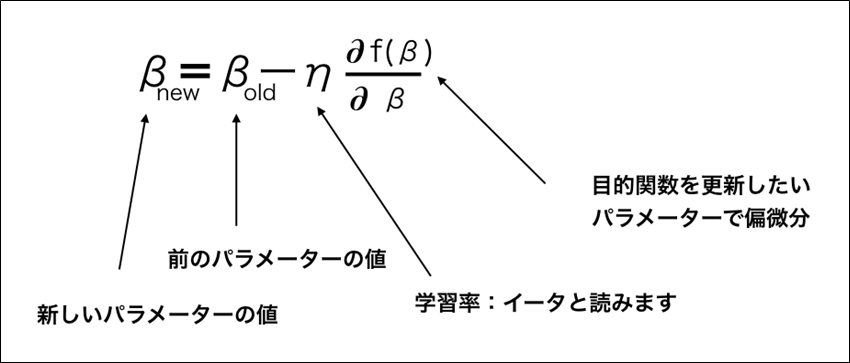
最小2乗法と最急降下法を用いて回帰直線を求めてみた

 

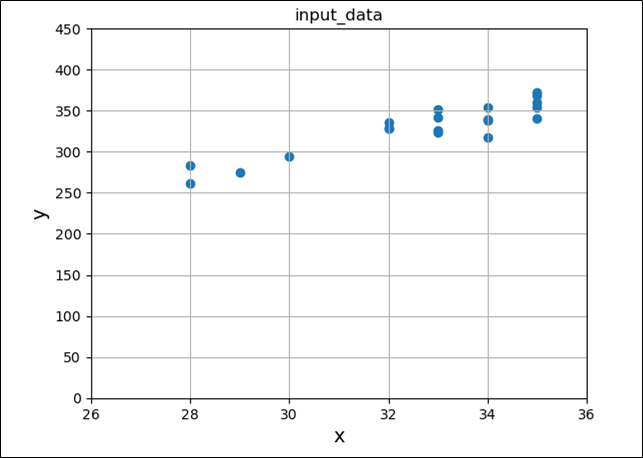
以下のように、入力データ\(x\),\(y\)の値が与えられた場合を考える。
前提条件_1

このときの、各点との距離が最小になるような\(y=ax+b\)という直線(=回帰直線)の傾き\(a\), 切片\(b\)を求めていく方法として、最小2乗法がある。
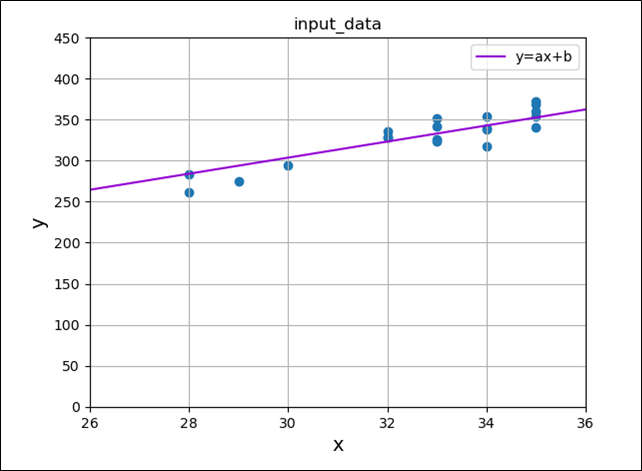
前提条件_2

最小2乗法とは、回帰直線と各点との距離の2乗和が最小になるような関係式を求める方法で、以下の計算結果を最小にする\(a\),\(b\)を求めればよい。
\[
\begin{eqnarray}
S &=& (ax_{1}+b-y_{1})^2 + (ax_{2}+b-y_{2})^2 + ･･･ + (ax_{n}+b-y_{n})^2 \\
&=& \sum_{i=1}^{n} (ax_{i}+b-y_{i})^2
\end{eqnarray}
\]

上記\(S\)の値を最小にする\(a\),\(b\)を求めるには、最急降下法で、以下の更新式を繰り返すことで求めることができる。ただし、今回は\(a\),\(b\)それぞれについて偏微分した更新式が必要になる。

最急降下法
出所：最急降下法の仕組みをイラストでわかりやすく解説

\(S\)を\(a\),\(b\)それぞれについて偏微分した式は以下のようになるため、この式を利用することになる。
\[
\begin{eqnarray}
\displaystyle \frac{\partial S}{\partial a} &=& 2\sum_{i=1}^{n} (ax_{i}+b-y_{i})x_{i} \\
\displaystyle \frac{\partial S}{\partial b} &=& 2\sum_{i=1}^{n} (ax_{i}+b-y_{i})
\end{eqnarray}
\]

なお、上記式の導出過程は、以下の記事を参照のこと。

最小2乗法の計算式を偏微分してみた このブログの以下の記事で、最小2乗法と最急降下法を用いて回帰直線を求めている。 https://www.purin-it.co...

今回は、最小2乗法と最急降下法を用いて、各点との距離が最小になるような\(y=ax+b\)という直線(=回帰直線)の傾き\(a\), 切片\(b\)を求めてみたので、そのサンプルプログラムを共有する。



前提条件

下記記事のAnacondaをインストールしJupyter Notebookを利用できること

Python開発用のAnacondaをインストールしJupyter Notebookを利用してみた今回は、Pythonを勉強してみたいと思い、Python開発環境を構築してみたので、その手順を共有する。 Python開発用として...

入力データx,yの値(全20個)を読み込み、散布図として表示すると、以下のようになる。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]

# 入力データを散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
plt.show()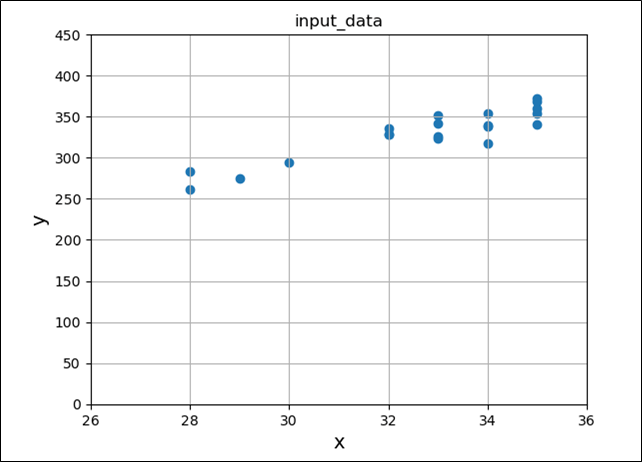
入力データの描画_実行結果

先ほど読み込んだ入力データの内容を出力した結果は、以下の通り。

import numpy as np		
		
# 入力データの読み込み		
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341], 
                       [35,360], [34,339], [32,329], [28,283], [35,372],		
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])		
# 入力データを出力		
print("*** 入力データ ***")		
print(input_data)		
print("*** 入力データの形状 ***")		
print(input_data.shape)		
		
# x座標、y座標の抜き出し		
input_data_x = input_data[:, 0]		
input_data_y = input_data[:, 1]		
		
# x座標、y座標を出力		
print("*** x座標 ***")		
print(input_data_x)		
print("*** y座標 ***")		
print(input_data_y)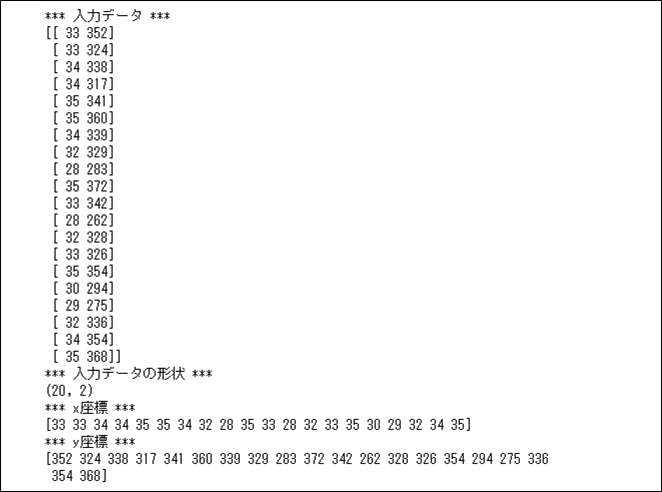
入力データ内容_実行結果

入力データを読み込み、\(a\),\(b\)に特定の値を設定した後で、\(\displaystyle \frac{\partial S}{\partial a} = 2\sum_{i=1}^{n} (ax_{i}+b-y_{i})x_{i}\)を(2*入力データ数)で除算した結果は、以下の通り。

%matplotlib inline
import matplotlib.pyplot as plt

def da_f(a, b, input_data):
    ret = 0
    input_data_cnt = input_data.shape[0]
    print("*** da_f(a, b, input_data)の呼び出し ***")
    print("input_data_cnt=" + str(input_data_cnt))
    for tmp in range(input_data_cnt):
        tmp_x = input_data[tmp, 0]
        tmp_y = input_data[tmp, 1]
        print("tmp=" + str(tmp) + ", tmp_x=" + str(tmp_x) + ", tmp_y=" + str(tmp_y))
        ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
    return ret

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# a,bの初期値
a = 10
b = 10

# 関数(da_f(a, b, input_data))を呼び出した場合の結果を確認
da_f(a, b, input_data)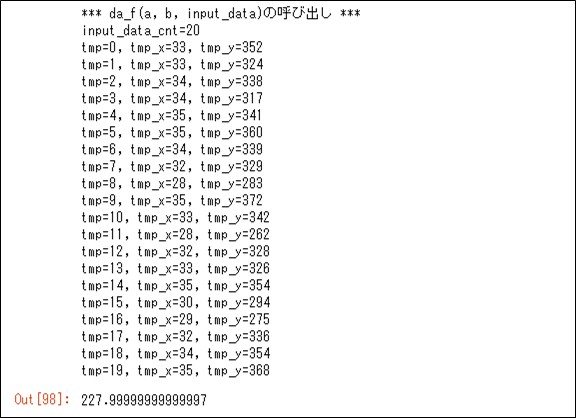
Sをaで偏微分した値の計算_実行結果

なお、\(S\)を\(a\)で偏微分した値を(2*入力データ数)で除算しているのは、計算結果をなるべく小さくするためである。また、\(S\)を\(b\)で偏微分した値も似たような式で計算できる。

最小2乗法と最急降下法を用いて、各点との距離が最小になるような\(y=ax+b\)という直線(=回帰直線)の傾き\(a\), 切片\(b\)を求めた後で、その結果をグラフで描画した結果は、以下の通り。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def da_f(a, b, input_data):
    ret = 0
    input_data_cnt = input_data.shape[0]
    for tmp in range(input_data_cnt):
        tmp_x = input_data[tmp, 0]
        tmp_y = input_data[tmp, 1]
        ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
    return ret

def db_f(a, b, input_data):
    ret = 0
    input_data_cnt = input_data.shape[0]
    for tmp in range(input_data_cnt):
        tmp_x = input_data[tmp, 0]
        tmp_y = input_data[tmp, 1]
        ret = ret + ( a * tmp_x + b - tmp_y ) / input_data_cnt
    return ret

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341], 
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]

# a,bの初期値
a = 10
b = 10
# 学習率η
eta = 0.0001

# 最急降下法を1,000回分繰り返した場合を確認
for num in range(1000):
    a = a - eta * da_f(a, b, input_data)
    b = b - eta * db_f(a, b, input_data)

# 最急降下法で計算後の値を確認
print("*** 最急降下法で計算後の各値 ***")
print("*** a,bの値 ***")
print("a = " + str(a) + ", b = " + str(b))
print("*** da_f(a, b, input_data)の値 ***")
print(da_f(a, b, input_data))
print("*** db_f(a, b, input_data)の値 ***")
print(db_f(a, b, input_data))

# 入力データの値を散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()

# 算出した直線(y=ax+b)を追加で表示
x = np.linspace(26, 36, 1000)
y = a * x + b
plt.plot(x, y, label='y=ax+b', color='darkviolet')
plt.legend()
plt.show()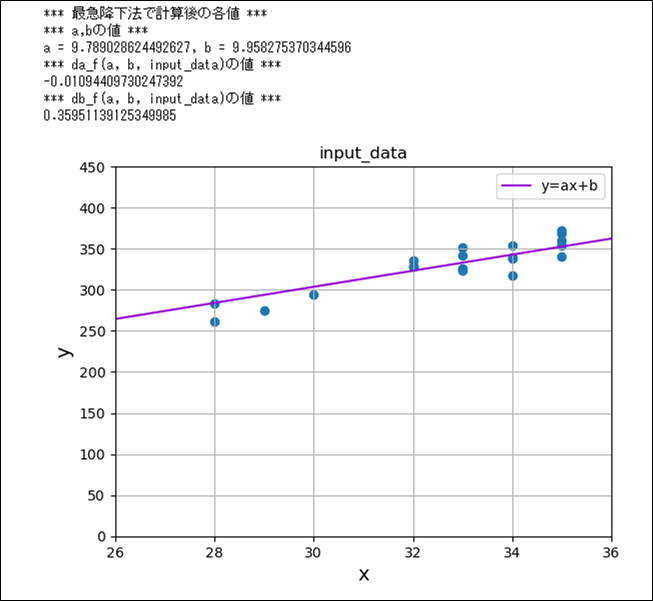
回帰直線の計算_実行結果

また、最急降下法の、更新式を1,000回繰り返した際の、(Sをaで偏微分した式を書く)(Sをbで偏微分した式を書く)の変化は以下の通りで、約50回の繰り返しで最小値に近づいているのが確認できる。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

def da_f(a, b, input_data):
    ret = 0
    input_data_cnt = input_data.shape[0]
    for tmp in range(input_data_cnt):
        tmp_x = input_data[tmp, 0]
        tmp_y = input_data[tmp, 1]
        ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
    return ret

def db_f(a, b, input_data):
    ret = 0
    input_data_cnt = input_data.shape[0]
    for tmp in range(input_data_cnt):
        tmp_x = input_data[tmp, 0]
        tmp_y = input_data[tmp, 1]
        ret = ret + ( a * tmp_x + b - tmp_y ) / input_data_cnt
    return ret

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341], 
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]

# a,bの初期値
a = 10
b = 10
# 学習率η
eta = 0.0001

# da_f, db_fの値の変化を格納
repeat_num = []
da_f_value = []
db_f_value = []

# 最急降下法を1,000回分繰り返した場合を確認
for num in range(1000):
    da_f_num = da_f(a, b, input_data)
    db_f_num = db_f(a, b, input_data)
    a = a - eta * da_f_num
    b = b - eta * db_f_num
    repeat_num.append(num)
    da_f_value.append(da_f_num)
    db_f_value.append(db_f_num)

# 最急降下法で計算後の値を確認
print("*** 最急降下法で計算後の各値 ***")
print("*** a,bの値 ***")
print("a = " + str(a) + ", b = " + str(b))
print("*** da_f(a, b, input_data)の値 ***")
print(da_f(a, b, input_data))
print("*** db_f(a, b, input_data)の値 ***")
print(db_f(a, b, input_data))

# da_fの値の変化(repeat_num,da_f_value)の値の変化をグラフ化
plt.plot(repeat_num, da_f_value)
plt.title("da_f value change")
plt.xlabel("repeat_num", size=14)
plt.ylabel("da_f_value", size=14)
plt.grid()
plt.show()

# db_fの値の変化(repeat_num,da_f_value)の値の変化をグラフ化
plt.plot(repeat_num, db_f_value)
plt.title("db_f value change")
plt.xlabel("repeat_num", size=14)
plt.ylabel("db_f_value", size=14)
plt.grid()
plt.show()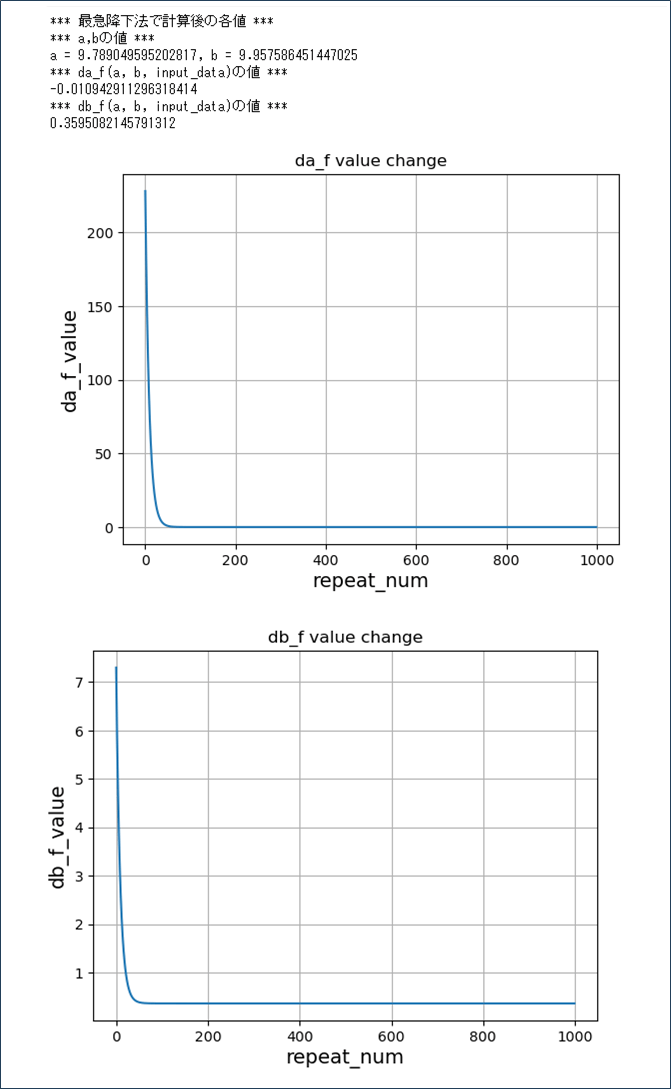
更新式を1,000回繰り返した際の偏微分の変化を表示_実行結果

要点まとめ

  • 各点との距離が最小になるようなy=ax+bという直線(=回帰直線)の傾きa, 切片bを求めていく方法として、最小2乗法がある。
  • 最小2乗法とは、回帰直線と各点との距離の2乗和が最小になるような関係式を求める方法をいい、この計算式を最小にするa,bの値は、最急降下法で求められる。
RELATED POST