機械学習

回帰直線の算出や標準化にscikit-learnを使ってみた

 

このブログの以下の記事で、最小2乗法と最急降下法を用いて回帰直線を求めている。

最小2乗法と最急降下法を用いて回帰直線を求めてみた 以下のように、入力データ\(x\),\(y\)の値が与えられた場合を考える。 このときの、各点との距離が最小になるような\...

また、以下の記事で、データの標準化を行っている。

回帰直線を求める際にデータを標準化してみた このブログの以下の記事で、最小2乗法と最急降下法を用いて回帰直線を求めている。 https://www.purin-it.co...

これらの記事の実装は、Python で利用できるデータ分析や機械学習のためのライブラリの一つであるscikit-learnを用いて行うこともできる。

今回は、scikit-learnのLinearRegressionクラスを用いた回帰直線の算出と、scikit-learnのStandardScalerクラスを用いたデータ標準化を行ってみたので、そのサンプルプログラムを共有する。

scikit-learnのLinearRegressionクラスを用いて回帰直線を算出した結果は、以下の通り。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341], 
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# LinearRegressionクラスを利用するため、抜き出したx座標・y座標を、
# 2次元1列の配列とする縦ベクトルに変更
input_data_x = input_data_x.reshape(-1, 1)
input_data_y = input_data_y.reshape(-1, 1)

# 入力データの値から、回帰直線を算出
clf = linear_model.LinearRegression()
clf.fit(input_data_x, input_data_y)

# 算出した回帰直線(y = ax+b)のa,bの値
a = clf.coef_[0][0]
b = clf.intercept_[0]
print("*** a,bの値 ***")
print("a = " + str(a) + ", b = " + str(b))

# 入力データの値を散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()

# 算出した直線(y = ax+b)を追加で表示
x = np.linspace(26, 36, 1000)
y = a * x + b
plt.plot(x, y, label='y = ax+b', color='darkviolet')
plt.legend()
plt.show()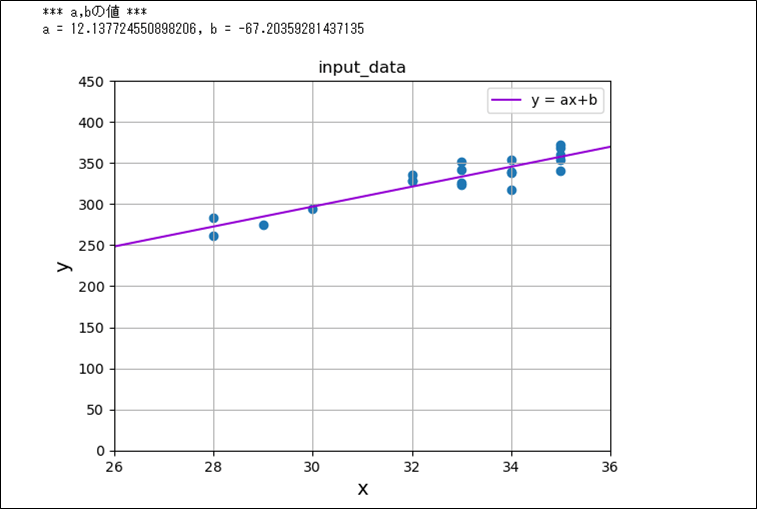
LinearRegressionクラスによる回帰直線の算出

また、scikit-learnのStandardScalerクラスを用いたデータ標準化／戻しを行った結果は、以下の通り。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341], 
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# 入力データの値を標準化
scaler = StandardScaler()
scaler.fit(input_data)
input_data_std = scaler.transform(input_data)

# 標準化後の入力データを元に戻す
input_data_rev = scaler.inverse_transform(input_data_std)

# 入力データの値を散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
plt.show()

# 入力データを標準化した値を散布図で表示
plt.scatter(input_data_std[:, 0], input_data_std[:, 1])
plt.title("input_data_std")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid()
plt.show()

# 入力データを標準化し戻した値を散布図で表示
plt.scatter(input_data_rev[:, 0], input_data_rev[:, 1])
plt.title("input_data_rev")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
plt.show()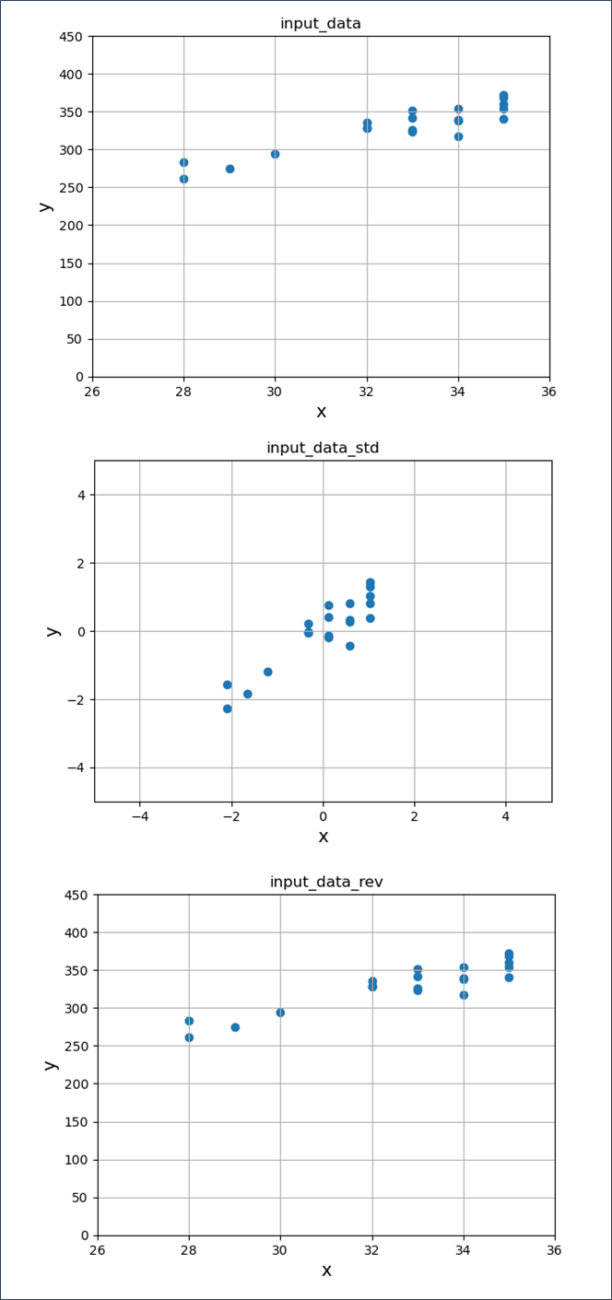
StandardScalerクラスによるデータ標準化／戻し

さらに、scikit-learnのLinearRegressionクラスとStandardScalerクラスを組み合わせた結果は、以下の通り。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn import linear_model

# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341], 
                       [35,360], [34,339], [32,329], [28,283], [35,372],
                       [33,342], [28,262], [32,328], [33,326], [35,354], 
                       [30,294], [29,275], [32,336], [34,354], [35,368]])

# 入力データの値を標準化
scaler = StandardScaler()
scaler.fit(input_data)
input_data_std = scaler.transform(input_data)

# 入力データ(標準化後)のx座標、y座標の抜き出し
input_data_std_x = input_data_std[:, 0]
input_data_std_y = input_data_std[:, 1]
# LinearRegressionクラスを利用するため、抜き出したx座標・y座標を、
# 2次元1列の配列とする縦ベクトルに変更
input_data_std_x = input_data_std_x.reshape(-1, 1)
input_data_std_y = input_data_std_y.reshape(-1, 1)

# 入力データ(標準化後)の値から、回帰直線を算出
clf = linear_model.LinearRegression()
clf.fit(input_data_std_x, input_data_std_y)

# 算出した回帰直線のa,bの値
a_std = clf.coef_[0][0]
b_std = clf.intercept_[0]
print("*** a,b(標準化後)の値 ***")
print("a = " + str(a_std) + ", b = " + str(b_std))

# 入力データ(標準化後)の値を散布図で表示
plt.scatter(input_data_std_x, input_data_std_y)
plt.title("input_data_std")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid()

# 算出した直線(y = a_std * x + b_std)を追加で表示
x = np.linspace(-5, 5, 1000)
y = a_std * x + b_std
plt.plot(x, y, label='y = a_std * x + b_std', color='darkviolet')
plt.legend()
plt.show()

# 標準化後に算出した直線(y = a_std * x + b_std)
input_data_rev = scaler.inverse_transform(np.column_stack([x, y]))

# 算出した直線(y = a_std * x + b_std)を標準化戻し後の、x座標、y座標の抜き出し
input_data_rev_x = input_data_rev[:, 0]
input_data_rev_y = input_data_rev[:, 1]
input_data_rev_x = input_data_rev_x.reshape(-1, 1)
input_data_rev_y = input_data_rev_y.reshape(-1, 1)

# 算出した直線(y = a_std * x + b_std)を標準化戻し後の、a,bの値を算出
clf2 = linear_model.LinearRegression()
clf2.fit(input_data_rev_x, input_data_rev_y)
a = clf2.coef_[0][0]
b = clf2.intercept_[0]
print("*** a,b(標準化前)の値 ***")
print("a = " + str(a) + ", b = " + str(b))

# 入力データの値(標準化前)を散布図で表示
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()

# 算出した直線(y = ax + b)を追加で表示
x_rev_line = input_data_rev[:, 0]
y_rev_line = input_data_rev[:, 1]
plt.plot(x_rev_line, y_rev_line, label='y=ax+b', color='darkviolet')
plt.legend()
plt.show()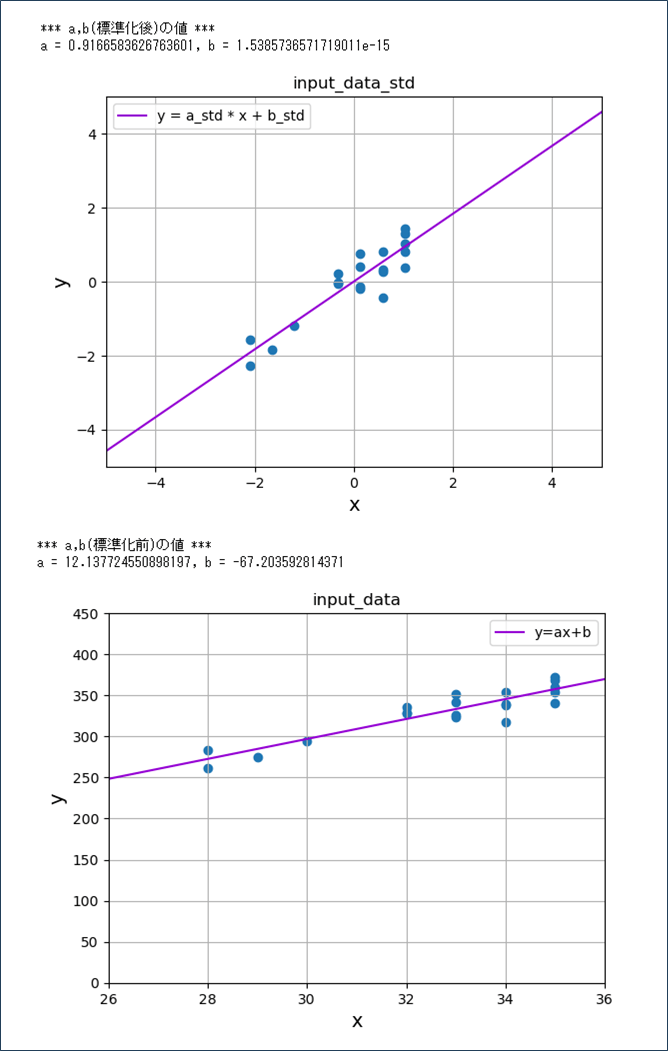
LinearRegressionクラスとStandardScalerクラスの併用

なお、正規化を行うscikit-learnのライブラリは、以下のサイトに記載のMinMaxScalerクラスとなる。
https://qiita.com/Qiitaman/items/c94420e8b86aae5f28a9

要点まとめ

  • Python で利用できるデータ分析や機械学習のためのライブラリの一つとして、scikit-learnがある。
  • 回帰直線の算出はscikit-learnのLinearRegressionクラスを、データの標準化はscikit-learnのStandardScalerクラスを、それぞれ利用して実施できる。
RELATED POST