このブログの以下の記事で、最小2乗法と最急降下法を用いて回帰直線を求めている。
最小2乗法と最急降下法を用いて回帰直線を求めてみた 以下のように、入力データ\(x\),\(y\)の値が与えられた場合を考える。 このときの、各点との距離が最小になるような\...
上記記事のように回帰直線を求める際、入力データが大きいと計算が難しくなるが、「正規化」や「標準化」の手法を利用すれば、入力データの値をあらかじめ小さく揃えておくことができる。
今回は、回帰直線を求める際に入力データを標準化してみたので、そのサンプルプログラムを共有する。
標準化とは、入力データの値の平均を0、標準偏差を1にする手法で、入力データのx座標を標準化するには、以下の公式を利用する。
出所：正規化・標準化を徹底解説
なお、平均・標準偏差については、以下の記事を参照のこと。
PythonのNumPyライブラリで平均・分散・標準偏差を求めてみた PythonのNumPyライブラリには、入力データとなる多次元配列(ndarray)の平均・分散・標準偏差を求める関数が用意されてい...
また、正規化と標準化の使い分けについては、以下のサイトの「標準化と正規化の使い分け」を参照のこと。
https://qiita.com/oki_kosuke/items/02ec7bee92c85cf10ac2
さらに、入力データのy座標も、同様の公式で標準化でき、以下のようになる。
\[
\begin{eqnarray}
y_{std}^i = \frac{y^i – μ_y}{σ_y}
\end{eqnarray}
\]
また、標準化した式を元に戻すには、先ほどの公式を以下のように変形し、\(x_i\)について解けばよい。
\[
\begin{eqnarray}
x_i – μ &=& x_{std}^i * σ \\
x_i &=& x_{std}^i * σ + μ
\end{eqnarray}
\]
y座標も同様に、\(y_i\)について解けばよい。
\[
\begin{eqnarray}
y_i = y_{std}^i * σ_y + μ_y
\end{eqnarray}
\]
標準化／標準化戻しの公式を利用して、入力データを標準化／標準化戻しを行った結果は以下の通りで、標準化した入力データは平均0・標準偏差1に近くなり、正規化戻しを行うと元に戻ることが確認できる。
import numpy as np
def standardize(input_data):
ave_val = np.mean(input_data)
std_val = np.std(input_data)
if std_val == 0:
return []
else:
return (input_data - ave_val) / std_val
def rev_standardize(input_data_std, ave_val, std_val):
return input_data_std * std_val + ave_val
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# x座標、y座標をそれぞれ標準化
input_data_x_std = standardize(input_data_x)
input_data_y_std = standardize(input_data_y)
# x座標、y座標(標準化後)を元に戻す
input_data_x_rev = rev_standardize(input_data_x_std
, np.mean(input_data_x), np.std(input_data_x))
input_data_y_rev = rev_standardize(input_data_y_std
, np.mean(input_data_y), np.std(input_data_y))
# 標準化したx座標、y座標の組み合わせを設定
input_data_std = np.column_stack([input_data_x_std,input_data_y_std])
# 標準化前後・標準化戻し前後の値を確認
print("*** 標準化前後・標準化戻し前後の各値 ***")
print("*** xの値(標準化前) ***")
print(input_data_x)
print("*** xの値(標準化後) ***")
print(input_data_x_std)
print("*** xの平均値(標準化後) ※0に近い ***")
print(np.mean(input_data_x_std))
print("*** xの標準偏差(標準化後) ※1に近い ***")
print(np.std(input_data_x_std))
print("*** xの値(標準化戻し後) ***")
print(input_data_x_rev)
print()
print("*** yの値(標準化前) ***")
print(input_data_y)
print("*** yの値(標準化後) ***")
print(input_data_y_std)
print("*** yの平均値(標準化後) ※0に近い ***")
print(np.mean(input_data_y_std))
print("*** yの標準偏差(標準化後) ※1に近い ***")
print(np.std(input_data_y_std))
print("*** yの値(標準化戻し後) ***")
print(input_data_y_rev)
print()
print("*** x,yの組み合わせ(標準化後) ***")
print(input_data_std)
さらに、入力データを標準化／標準化戻しをグラフ化した結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def standardize(input_data):
ave_val = np.mean(input_data)
std_val = np.std(input_data)
if std_val == 0:
return []
else:
return (input_data - ave_val) / std_val
def rev_standardize(input_data_std, ave_val, std_val):
return input_data_std * std_val + ave_val
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# x座標、y座標をそれぞれ標準化
input_data_x_std = standardize(input_data_x)
input_data_y_std = standardize(input_data_y)
# x座標、y座標(標準化後)を元に戻す
input_data_x_rev = rev_standardize(input_data_x_std
, np.mean(input_data_x), np.std(input_data_x))
input_data_y_rev = rev_standardize(input_data_y_std
, np.mean(input_data_y), np.std(input_data_y))
# 入力データの値を散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
plt.show()
# 入力データを標準化した値を散布図で表示
plt.scatter(input_data_x_std, input_data_y_std)
plt.title("input_data_std")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid()
plt.show()
# 入力データを標準化し戻した値を散布図で表示
plt.scatter(input_data_x_rev, input_data_y_rev)
plt.title("input_data_rev")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
plt.show()
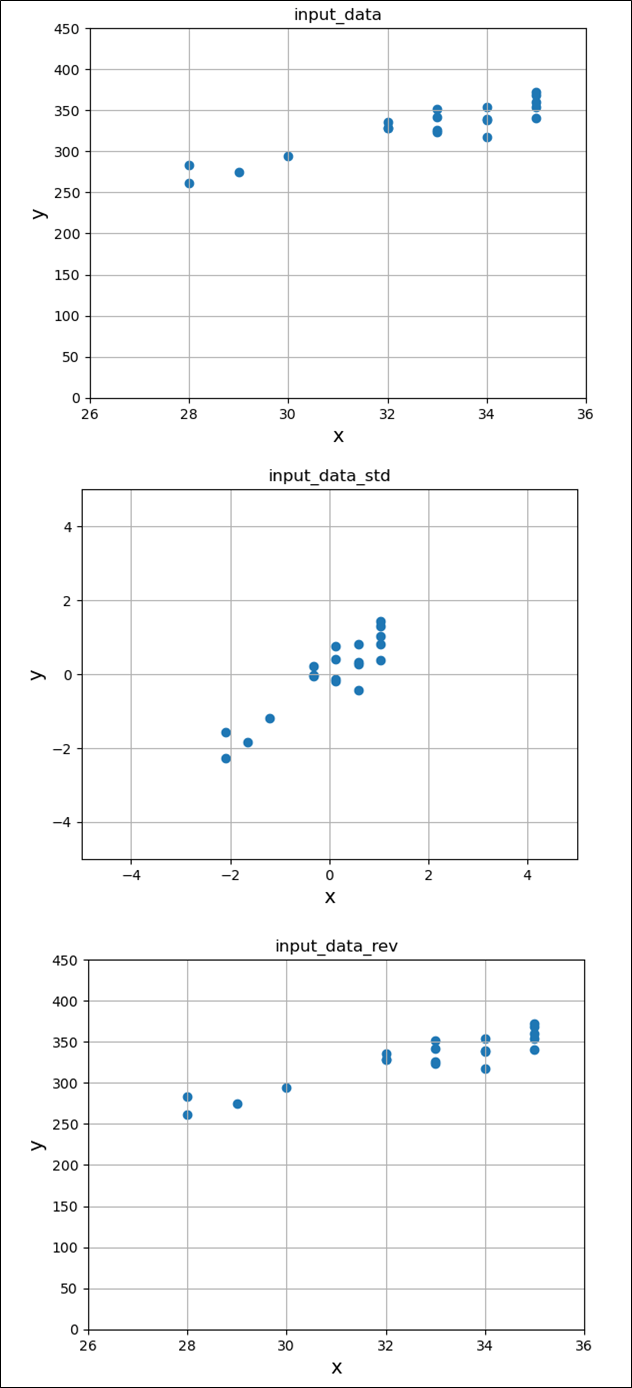
次に、入力データを標準化した後で、最小2乗法と最急降下法を用いて回帰直線を求めた結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def standardize(input_data):
ave_val = np.mean(input_data)
std_val = np.std(input_data)
if std_val == 0:
return []
else:
return (input_data - ave_val) / std_val
def rev_standardize(input_data_std, ave_val, std_val):
return input_data_std * std_val + ave_val
def da_f(a, b, input_data):
ret = 0
input_data_cnt = input_data.shape[0]
for tmp in range(input_data_cnt):
tmp_x = input_data[tmp, 0]
tmp_y = input_data[tmp, 1]
ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
return ret
def db_f(a, b, input_data):
ret = 0
input_data_cnt = input_data.shape[0]
for tmp in range(input_data_cnt):
tmp_x = input_data[tmp, 0]
tmp_y = input_data[tmp, 1]
ret = ret + ( a * tmp_x + b - tmp_y ) / input_data_cnt
return ret
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# x座標、y座標をそれぞれ標準化
input_data_x_std = standardize(input_data_x)
input_data_y_std = standardize(input_data_y)
input_data_std = np.column_stack([input_data_x_std, input_data_y_std])
# a,b(標準化後)の初期値
a_std = 1
b_std = 1
# 学習率η
eta = 0.001
# 最急降下法を10,000回分繰り返した場合を確認
for num in range(10000):
a_std = a_std - eta * da_f(a_std, b_std, input_data_std)
b_std = b_std - eta * db_f(a_std, b_std, input_data_std)
# a,b(標準化後)の値を表示
print("*** a,b(標準化後)の値 ***")
print("a_std = " + str(a_std) + ", b_std = " + str(b_std))
# 入力データの値(標準化後)を散布図で表示
plt.scatter(input_data_x_std, input_data_y_std)
plt.title("input_data_std")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid()
# 算出した直線(y_std = a_std * x_std + b_std)を追加で表示
x_std = np.linspace(-5, 5, 1000)
y_std = a_std * x_std + b_std
plt.plot(x_std, y_std, label='y = a_std * x + b_std', color='darkviolet')
plt.legend()
plt.show()
# 入力データの値(標準化前)を散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = a_std * x + b_std)を標準化後の値に戻し、追加で表示
x_rev = rev_standardize(x_std, np.mean(input_data_x), np.std(input_data_x))
y_rev = rev_standardize(y_std, np.mean(input_data_y), np.std(input_data_y))
plt.plot(x_rev, y_rev, label='y=ax+b', color='darkviolet')
plt.legend()
plt.show()
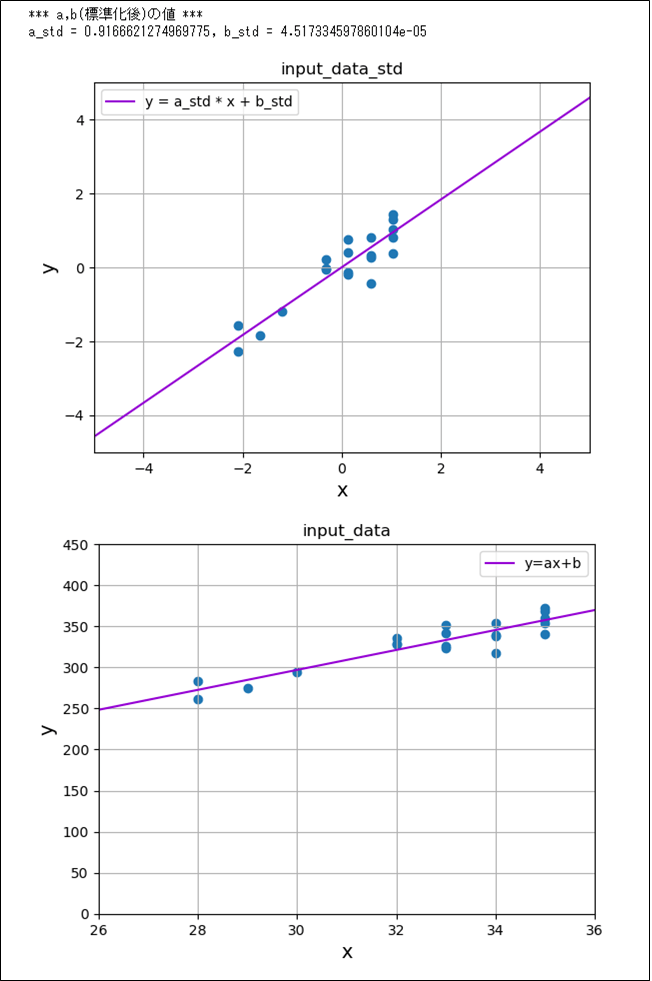
なお、最小2乗法と最急降下法を用いて回帰直線を求める方法については、以下の記事を参照のこと。
最小2乗法と最急降下法を用いて回帰直線を求めてみた 以下のように、入力データ\(x\),\(y\)の値が与えられた場合を考える。 このときの、各点との距離が最小になるような\...
さらに、標準化後の回帰直線(\(y=ax+b\))の\(a\),\(b\)の値も算出することができる。その算出方法は、以下の通り。
\[
\begin{eqnarray}
\frac{y – μ_y}{σ_y} &=& a_{std} * \frac{x – μ_x}{σ_x} + b_{std} \\
y – μ_y &=& a_{std} * σ_y * \frac{x – μ_x}{σ_x} + b_{std} * σ_y \\
y &=& a_{std} * σ_y * \frac{x – μ_x}{σ_x} + b_{std} * σ_y + μ_y \\
y &=& a_{std} * \frac{σ_y}{σ_x} * x – a_{std} * σ_y * \frac{μ_x}{σ_x} + b_{std} * σ_y + μ_y
\end{eqnarray}
\]
以上より、
\[
\begin{eqnarray}
a &=& a_{std} * \frac{σ_y}{σ_x} \\
b &=& – a_{std} * σ_y * \frac{μ_x}{σ_x} + b_{std} * σ_y + μ_y
\end{eqnarray}
\]
となる。
実際に、標準化後の回帰直線(\(y=ax+b\))の\(a\),\(b\)の値を計算し、グラフ化した結果は、以下の通り。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def standardize(input_data):
ave_val = np.mean(input_data)
std_val = np.std(input_data)
if std_val == 0:
return []
else:
return (input_data - ave_val) / std_val
def da_f(a, b, input_data):
ret = 0
input_data_cnt = input_data.shape[0]
for tmp in range(input_data_cnt):
tmp_x = input_data[tmp, 0]
tmp_y = input_data[tmp, 1]
ret = ret + (( a * tmp_x + b - tmp_y ) * tmp_x) / input_data_cnt
return ret
def db_f(a, b, input_data):
ret = 0
input_data_cnt = input_data.shape[0]
for tmp in range(input_data_cnt):
tmp_x = input_data[tmp, 0]
tmp_y = input_data[tmp, 1]
ret = ret + ( a * tmp_x + b - tmp_y ) / input_data_cnt
return ret
# 入力データの読み込み
input_data = np.array([[33,352], [33,324], [34,338], [34,317], [35,341],
[35,360], [34,339], [32,329], [28,283], [35,372],
[33,342], [28,262], [32,328], [33,326], [35,354],
[30,294], [29,275], [32,336], [34,354], [35,368]])
# x座標、y座標の抜き出し
input_data_x = input_data[:, 0]
input_data_y = input_data[:, 1]
# x座標、y座標をそれぞれ標準化
input_data_x_std = standardize(input_data_x)
input_data_y_std = standardize(input_data_y)
input_data_std = np.column_stack([input_data_x_std, input_data_y_std])
# a,b(標準化後)の初期値
a_std = 1
b_std = 1
# 学習率η
eta = 0.001
# 最急降下法を10,000回分繰り返した場合を確認
for num in range(10000):
a_std = a_std - eta * da_f(a_std, b_std, input_data_std)
b_std = b_std - eta * db_f(a_std, b_std, input_data_std)
# a,b(標準化後)の値を表示
print("*** a,b(標準化後)の値 ***")
print("a_std = " + str(a_std) + ", b_std = " + str(b_std))
# 入力データの値(標準化後)を散布図で表示
plt.scatter(input_data_x_std, input_data_y_std)
plt.title("input_data_std")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(-5, 5)
plt.ylim(-5, 5)
plt.grid()
# 算出した直線(y_std = a_std * x_std + b_std)を追加で表示
x_std = np.linspace(-5, 5, 1000)
y_std = a_std * x_std + b_std
plt.plot(x_std, y_std, label='y = a_std * x + b_std', color='darkviolet')
plt.legend()
plt.show()
# 入力データの値(標準化前)の平均・標準偏差を算出
x_ave = np.mean(input_data_x)
x_stdd = np.std(input_data_x)
y_ave = np.mean(input_data_y)
y_stdd = np.std(input_data_y)
# 算出した直線(y = a_std * x + b_std)を標準化戻し後の、a,bの値を算出
a = a_std * y_stdd / x_stdd
b = -a_std * y_stdd * x_ave / x_stdd + b_std * y_stdd + y_ave
print("*** a,b(標準化前)の値 ***")
print("a = " + str(a) + ", b = " + str(b))
# 入力データの値(標準化前)を散布図で表示
plt.scatter(input_data_x, input_data_y)
plt.title("input_data")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.xlim(26, 36)
plt.ylim(0, 450)
plt.grid()
# 算出した直線(y = ax + b)を追加で表示
x_rev_line = np.linspace(26, 36, 1000)
y_rev_line = a*x_rev_line + b
plt.plot(x_rev_line, y_rev_line, label='y=ax+b', color='darkviolet')
plt.legend()
plt.show()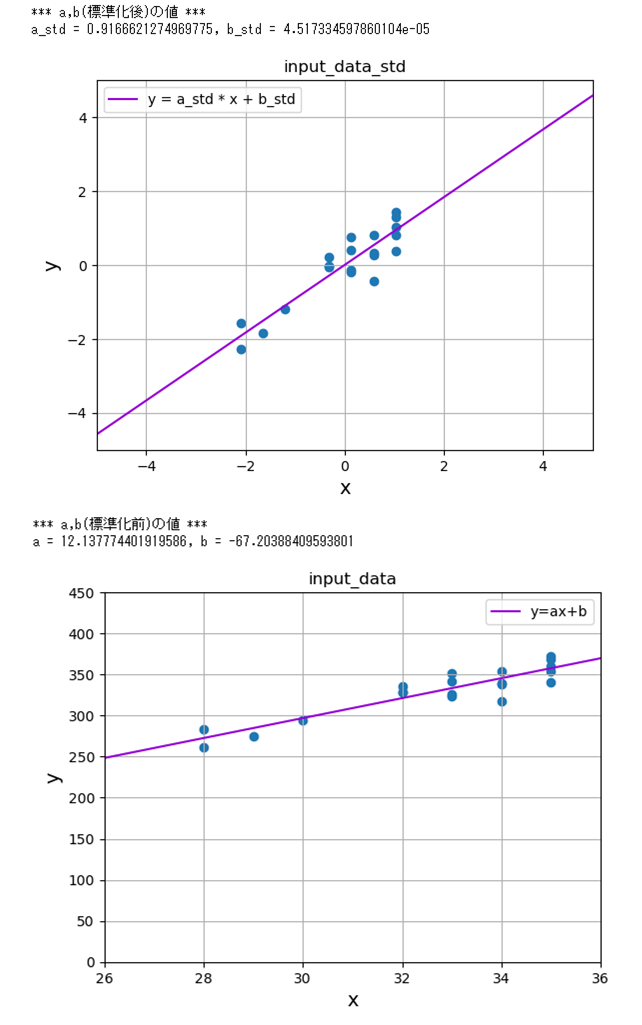
要点まとめ
- 回帰直線を求める際、入力データが大きいと計算が難しくなるが、「正規化」や「標準化」の手法を利用すれば、入力データの値をあらかじめ小さく揃えておくことができる。
- 標準化とは、入力データの値の平均を0、標準偏差を1にする手法のことをいう。
