tanh関数とその微分をグラフ化してみた｜ITエンジニアとして経験・学習したこと

\(tanh(x)=\displaystyle \frac{e^x – e^{-x}}{e^x + e^{-x}}\)で表現される関数をtanh(ハイパボリックタンジェント)関数といい、ディープラーニングの活性化関数の1つとして利用される。

今回は、tanh関数とその微分をグラフ化してみたので、その結果を共有する。

\(tanh(x)=\displaystyle \frac{e^x – e^{-x}}{e^x + e^{-x}}\)をPythonでグラフ化した結果は、以下の通り。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# tanh関数の定義
def tanh(x):
    return (np.e**(x) - np.e**(-x)) / (np.e**(x) + np.e**(-x))

# -10～10までを1000等分した値をxとする
x = np.linspace(-10, 10, 1000)
# 上記xに対応する標準シグモイド関数yの値を算出
y = tanh(x)

# x,yに対応する値のグラフを表示
plt.plot(x, y)
plt.title("tanh function")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.grid()
plt.show()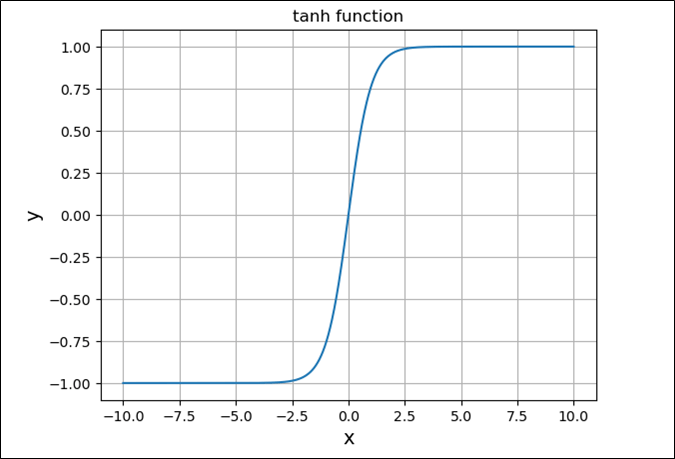

%matplotlib inline

import numpy as np

import matplotlib.pyplot as plt

# tanh関数の定義

def tanh(x):

return (np.e**(x) - np.e**(-x)) / (np.e**(x) + np.e**(-x))

# -10～10までを1000等分した値をxとする

x = np.linspace(-10, 10, 1000)

# 上記xに対応する標準シグモイド関数yの値を算出

y = tanh(x)

# x,yに対応する値のグラフを表示

plt.plot(x, y)

plt.title("tanh function")

plt.xlabel("x", size=14)

plt.ylabel("y", size=14)

plt.grid()

plt.show()

「HD Video Converter Factory Pro」は動画の形式変換や編集・録画等を行える便利ツールだった動画の形式変換や編集・録画等を行える便利ツールの一つに、「HD Video Converter Factory Pro」があります。ここ...

また、\(tanh(x)=\displaystyle \frac{e^x – e^{-x}}{e^x + e^{-x}}\)を\(x\)について微分すると、以下のようになる。
\[
\begin{eqnarray}
\displaystyle \frac{d}{dx} tanh(x) &=& \displaystyle \frac{\displaystyle \frac{d}{dx} (e^x – e^{-x})(e^x + e^{-x}) – \frac{d}{dx}(e^x + e^{-x})(e^x – e^{-x}) }{({e^x + e^{-x}})^2} \\
&=& \displaystyle \frac{(e^x + e^{-x})(e^x + e^{-x}) – (e^x – e^{-x})(e^x – e^{-x})}{({e^x + e^{-x}})^2} \\
&=& \displaystyle \frac{(e^x + e^{-x})^2 – (e^x – e^{-x})^2}{({e^x + e^{-x}})^2} \\
&=& \displaystyle \frac{(e^{2x} + 2 \times e^x \times e^{-x} + e^{-2x}) – (e^{2x} – 2 \times e^x \times e^{-x} – e^{-2x})}{({e^x + e^{-x}})^2} \\
&=& \displaystyle \frac{(e^{2x} + 2 + e^{-2x}) – (e^{2x} – 2 – e^{-2x})}{({e^x + e^{-x}})^2} \\
&=& \displaystyle \frac{e^{2x} + 2 + e^{-2x} – e^{2x} + 2 – e^{-2x}}{({e^x + e^{-x}})^2} = \displaystyle \frac{4}{({e^x + e^{-x}})^2}
\end{eqnarray}
\]

なお、上記計算にあたっては、以下のサイトの「分数関数の微分公式」と、\(e^x\)が微分しても\(e^x\)であることを利用している。
https://manabitimes.jp/math/2047

上記、tanh関数の微分をグラフに追加した結果は、以下の通り。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

# tanh関数の定義
def tanh(x):
    return (np.e**(x) - np.e**(-x)) / (np.e**(x) + np.e**(-x))

# tanh関数の微分の定義
def diff_tanh(x):
    return 4 / (np.e**(x) + np.e**(-x))**2

# -10～10までを1000等分した値をxとする
x = np.linspace(-10, 10, 1000)
# 上記xに対応する標準シグモイド関数y1の値を算出
y1 = tanh(x)
# 上記xに対応する標準シグモイド関数の微分y2の値を算出
y2 = diff_tanh(x)

# x,y1,y2に対応する値のグラフを表示
plt.plot(x, y1, label='tanh')
plt.plot(x, y2, label='tanh differential')
plt.title("tanh function and differential")
plt.xlabel("x", size=14)
plt.ylabel("y", size=14)
plt.legend()
plt.grid()
plt.show()

%matplotlib inline

import numpy as np

import matplotlib.pyplot as plt

# tanh関数の定義

def tanh(x):

return (np.e**(x) - np.e**(-x)) / (np.e**(x) + np.e**(-x))

# tanh関数の微分の定義

def diff_tanh(x):

return 4 / (np.e**(x) + np.e**(-x))**2

# -10～10までを1000等分した値をxとする

x = np.linspace(-10, 10, 1000)

# 上記xに対応する標準シグモイド関数y1の値を算出

y1 = tanh(x)

# 上記xに対応する標準シグモイド関数の微分y2の値を算出

y2 = diff_tanh(x)

# x,y1,y2に対応する値のグラフを表示

plt.plot(x, y1, label='tanh')

plt.plot(x, y2, label='tanh differential')

plt.title("tanh function and differential")

plt.xlabel("x", size=14)

plt.ylabel("y", size=14)

plt.legend()

plt.grid()

plt.show()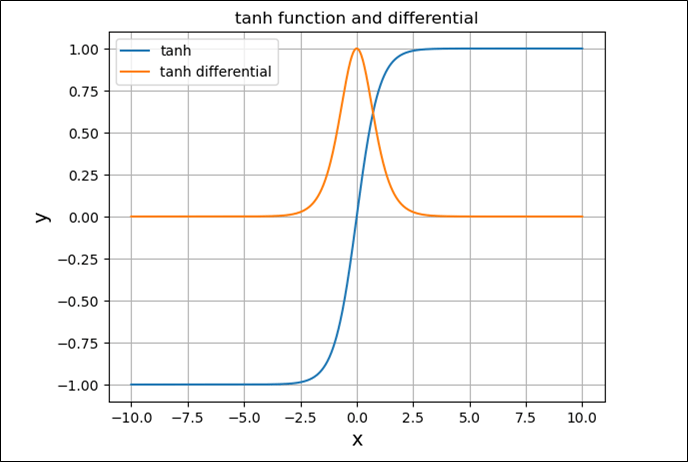

要点まとめ

\(tanh(x)=\displaystyle \frac{e^x – e^{-x}}{e^x + e^{-x}}\)で表現される関数をtanh(ハイパボリックタンジェント)関数といい、ディープラーニングの活性化関数の1つとして利用される。
\(tanh(x)=\displaystyle \frac{e^x – e^{-x}}{e^x + e^{-x}}\)を微分すると、\(\displaystyle \frac{4}{({e^x + e^{-x}})^2}\)となる。