入力データが正規分布に従うと仮定した場合の外れ値の検出方法の1つに「3σ法」がある。
3σ法は、σを標準偏差として、(平均)-3σ～(平均)+3σの範囲(全体の約99.7%)から外れたデータを外れ値とする方法で、製造業等でよく使われている。
今回は、3σ法で外れ値を除去してみたので、そのサンプルプログラムを共有する。
なお、3σ法の詳細は、以下のサイトを参照のこと。
https://www.env.go.jp/chemi/rhm/r1kisoshiryo/r1kiso-02-04-04.html
また、正規分布については、以下のサイトを参照のこと。
正規分布の計算を行いグラフを描いてみた 正規分布は連続型の確率分布(=確率密度関数)の1つで、世の中の多くの分布が正規分布に従うといわれている。 平均\(μ\)、分散...
Numpyのnumpy.randomモジュールのnormalメソッドを利用すると、指定した数だけ、正規分布に従う乱数を作成できる。
標準正規分布に従う乱数を10,000個作成しグラフ化した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 平均ave=0,標準偏差std=1 ave = 0 std = 1 # 標準正規分布(平均ave=0,標準偏差std=1)に従う # ランダムな値を10000件生成 data = np.random.normal(ave, std, 10000) # 生成されたdataの確認 print("*** dataの型 ***") print(type(data)) print("*** dataの長さ ***") print(len(data)) print("*** dataの平均、標準偏差 ***") print("平均：" + str(np.mean(data)) + ", 標準偏差：" + str(np.std(data))) print() print("*** data 最初の5件 ***") print(str(data[0]) + ", " + str(data[1]) + ", " + str(data[2]) + ", " + str(data[3]) + ", " + str(data[4])) print("*** data 末尾の5件 ***") print(str(data[9995]) + ", " + str(data[9996]) + ", " + str(data[9997]) + ", " + str(data[9998]) + ", " + str(data[9999])) # 生成されたdata10000件のグラフを表示 plt.hist(data, bins=50) plt.title("normal distribution graph") plt.xlabel("data", size=14) plt.ylabel("data count", size=14) plt.grid() plt.show() |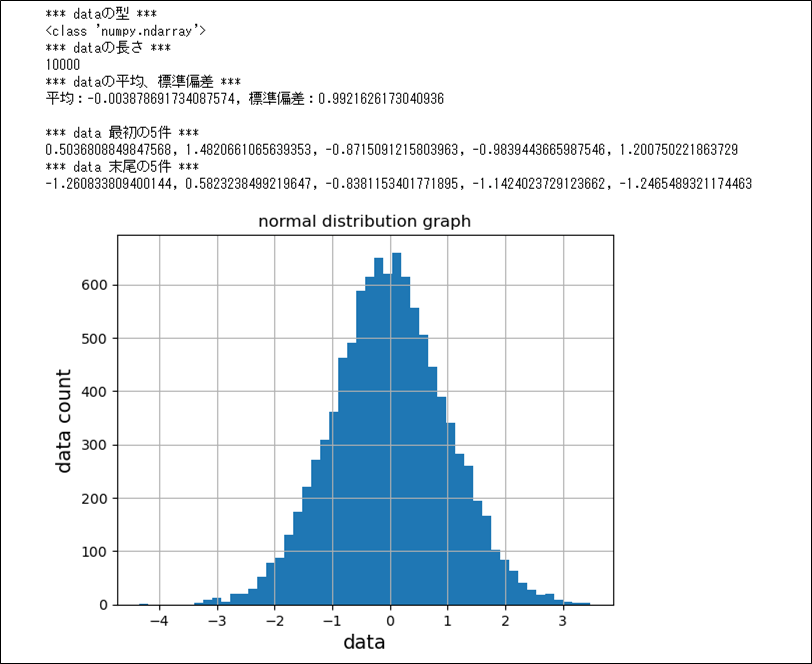
次に、3σ法で外れ値となるデータを追加する。データ追加前／追加後のデータを表示した結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # 平均ave=0,標準偏差std=1 ave = 0 std = 1 # 標準正規分布(平均ave=0,標準偏差std=1)に従うランダムな値を28件生成 data = np.random.normal(ave, std, 28) # print(data)を表示する際、小数点以下3桁まで＋指数表記しない形式に設定 np.set_printoptions(precision=3, suppress=True) # 生成されたdataの確認 print("*** 3σ法で外れ値となるデータ追加前 ***") print("*** dataの内容 ***") print(data) print("*** dataの長さ ***") print(len(data)) print("*** dataの平均、標準偏差 ***") print("平均：" + str(np.mean(data)) + ", 標準偏差：" + str(np.std(data))) # dataのグラフを表示 plt.hist(data) plt.title("before add two outlier datas") plt.xlabel("data", size=14) plt.ylabel("data count", size=14) plt.grid() plt.show() |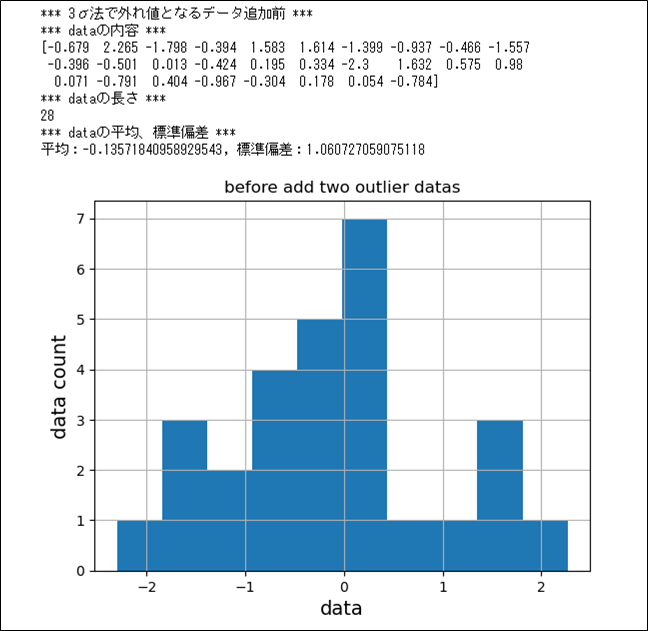
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt # ave-3*std～ave+3*stdにあてはまらない(3σ法で除去対象となる)データを2件追加 data = np.append(data, -29) data = np.append(data, 30) # print(data)を表示する際、小数点以下3桁まで＋指数表記しない形式に設定 np.set_printoptions(precision=3, suppress=True) # 生成されたdataの確認 print("*** 3σ法で外れ値となるデータ追加後 ***") print("*** dataの内容 ***") print(data) print("*** dataの長さ ***") print(len(data)) print("*** dataの平均、標準偏差 ***") print("平均：" + str(np.mean(data)) + ", 標準偏差：" + str(np.std(data))) # dataのグラフを表示 plt.hist(data) plt.title("after add two outlier datas") plt.xlabel("data", size=14) plt.ylabel("data count", size=14) plt.grid() plt.show() |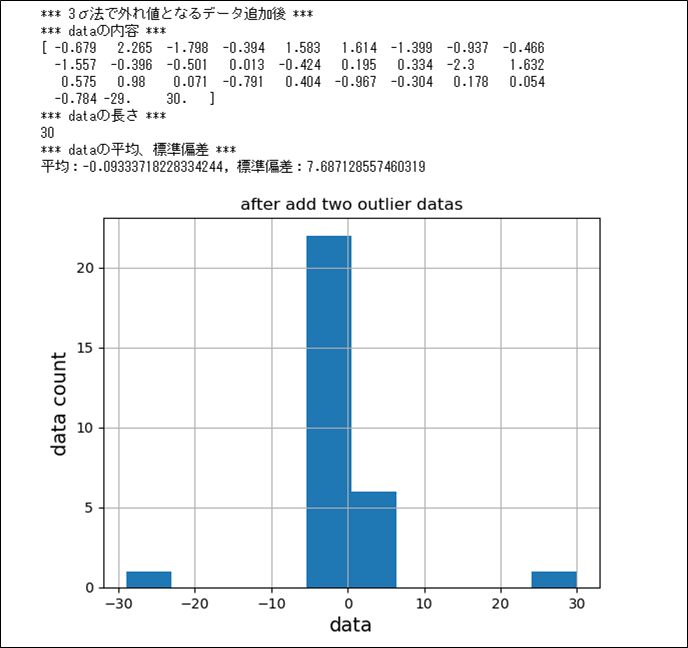
さらに、Pandasを利用して、3σ法で外れ値となるデータを削除する。その結果は、以下の通り。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | %matplotlib inline import numpy as np import matplotlib.pyplot as plt import pandas as pd # dataをPandasのDataFrameに変換 df = pd.DataFrame(data) # ave-3*std～ave+3*stdにあてはまらない(3σ法で除去対象とならない)範囲を表示 ave = np.mean(data) std = np.std(data) low = ave - 3*std high = ave + 3*std print("*** 残すデータの最小値・最大値 ***") print("最小値：" + str(low) + ", 最大値：" + str(high)) print() # ave-3*std～ave+3*stdにあてはまらない(3σ法で除去対象となる)データを削除し、 # dataを(1次元の)NumPy配列に変換 df = df[(df[0] > low) & (df[0] < high)] data = df.values.flatten() # print(data)を表示する際、小数点以下3桁まで＋指数表記しない形式に設定 np.set_printoptions(precision=3, suppress=True) # 生成されたdataの確認 print("*** 3σ法で外れ値となるデータ削除後 ***") print("*** dataの内容 ***") print(data) print("*** dataの長さ ***") print(len(data)) print("*** dataの平均、標準偏差 ***") print("平均：" + str(np.mean(data)) + ", 標準偏差：" + str(np.std(data))) # dataのグラフを表示 plt.hist(data) plt.title("after remove two outlier datas") plt.xlabel("data", size=14) plt.ylabel("data count", size=14) plt.grid() plt.show() |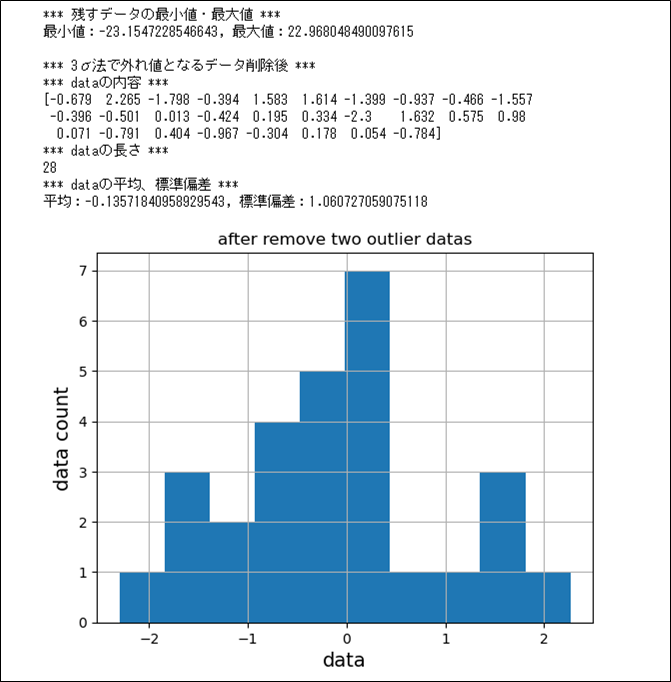
要点まとめ
- 入力データが正規分布に従うと仮定した場合の外れ値の検出方法の1つに「3σ法」があり、3σ法では、σを標準偏差として、(平均)-3σ～(平均)+3σの範囲(全体の約99.7%)から外れたデータを外れ値とする。
